বিন্যাস হল বস্তু গুলিকে একটি নির্দিষ্ট ক্রমে সাজানো। এর জন্য সূত্র:
\[
P(n, r) = \frac{n!}{(n - r)!}
\]
সমাবেশ হল বস্তু গুলিকে বেছে নেওয়া, যেখানে ক্রমের কোনো গুরুত্ব নেই। এর জন্য সূত্র:
\[
C(n, r) = \frac{n!}{r!(n - r)!}
\]
নির্ণায়ক একটি ম্যাট্রিক্সের গুণমান। এটি ম্যাট্রিক্সের বিভিন্ন বৈশিষ্ট্য নির্ধারণে সাহায্য করে।
ম্যাট্রিক্স হল সংখ্যার একটি গাণিতিক কাঠামো যা লিনিয়ার সমীকরণ সমাধান বা ডেটা ব্যবস্থাপনায় ব্যবহৃত হয়।
কোনো এক শ্রেণিকক্ষের 25 জন ছাত্রের মধ্য হতে 6 জন ছাত্রকে কাবাডি খেলার জন্য নির্বাচন করা হলো।
তথ্যবিশ্ব, Y=2, 4, 6, 8 হতে পুনঃস্থান করে 2 আকারের নমুনা নির্বাচন করা হলো।
বিন্যাস হল এমন একটি পরিসংখ্যানিক ধারণা যেখানে নির্দিষ্ট সংখ্যা বা বস্তু একত্রিত করার পদ্ধতি নির্ধারণ করা হয়, যেখানে বস্তু গুলির ক্রম (order) গুরুত্বপূর্ণ।
বিন্যাসের সূত্র:
\[
P(n, r) = \frac{n!}{(n - r)!}
\]
এখানে,
ধরা যাক, একটি বাক্সে 5টি বল রয়েছে (A, B, C, D, E)। এর মধ্যে 3টি বল বেছে নিয়ে তাদের সাজানোর উপায় সংখ্যা কত হবে?
এক্ষেত্রে, \(n = 5\) এবং \(r = 3\) হবে। তাই,
\[
P(5, 3) = \frac{5!}{(5 - 3)!} = \frac{5 \times 4 \times 3!}{2!} = 5 \times 4 \times 3 = 60
\]
অর্থাৎ, 5টি বস্তু থেকে 3টি বস্তু বাছাই ও সাজানোর মোট 60টি উপায় রয়েছে।
সমাবেশ হলো বস্তু গুলিকে এমনভাবে নির্বাচন করা, যেখানে তাদের মধ্যে কোনো নির্দিষ্ট ক্রম (order) থাকে না। এটি মূলত বস্তু গুলির নির্বাচন নির্ধারণ করে, যেগুলির মধ্যে কোনো ক্রমের গুরুত্ব নেই।
সমাবেশের সূত্র:
\[
C(n, r) = \frac{n!}{r!(n - r)!}
\]
এখানে,
ধরা যাক, একটি বাক্সে 5টি বল রয়েছে (A, B, C, D, E)। এর মধ্যে 3টি বল বেছে নেয়ার উপায় সংখ্যা কত হবে?
এক্ষেত্রে, \(n = 5\) এবং \(r = 3\) হবে। তাহলে,
\[
C(5, 3) = \frac{5!}{3!(5 - 3)!} = \frac{5 \times 4 \times 3!}{3! \times 2!} = \frac{5 \times 4}{2 \times 1} = 10
\]
অর্থাৎ, 5টি বস্তু থেকে 3টি বস্তু বাছাই করার 10টি উপায় রয়েছে।
নির্ণায়ক (Determinant) একটি ম্যাট্রিক্সের গুণমান বা বৈশিষ্ট্য নির্ধারণকারী একটি সংখ্যা। এটি ম্যাট্রিক্সের বিভিন্ন বৈশিষ্ট্য যেমন সমীকরণের সমাধান, বিপরীত ম্যাট্রিক্স (inverse), এবং অন্যান্য গাণিতিক অপারেশন নির্ধারণে ব্যবহৃত হয়।
ধরা যাক, একটি ২x২ ম্যাট্রিক্স \( A \) আছে:
\[
A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}
\]
এর নির্ণায়ক হবে:
\[
\text{det}(A) = ad - bc
\]
ধরা যাক, একটি ৩x৩ ম্যাট্রিক্স \( A \) আছে:
\[
A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}
\]
এর নির্ণায়ক হবে:
\[
\text{det}(A) = a(ei - fh) - b(di - fg) + c(dh - eg)
\]
ধরা যাক, একটি ২x২ ম্যাট্রিক্স \( A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \) দেওয়া আছে।
তাহলে, এর নির্ণায়ক হবে:
\[
\text{det}(A) = 1(4) - 2(3) = 4 - 6 = -2
\]
নির্ণায়ক একাধিক গাণিতিক প্রয়োগে ব্যবহৃত হয়, যেমন সমীকরণের সমাধান, ইনভার্স ম্যাট্রিক্স খোঁজা, ইত্যাদি।
নির্ণায়কের কিছু গুরুত্বপূর্ণ গুণাবলী রয়েছে যা ম্যাট্রিক্সের বিভিন্ন গাণিতিক কার্যক্রম এবং বৈশিষ্ট্য বুঝতে সাহায্য করে। এখানে নির্ণায়কের কিছু মৌলিক গুণাবলী এবং সেগুলির প্রমাণ দেওয়া হল:
যদি \( A \) একটি \( n \times n \) ম্যাট্রিক্স হয় এবং আমরা এর দুটি সারি (বা কলাম) বিনিময় করি, তবে নির্ণায়ক পরিবর্তিত হবে। অর্থাৎ,
\[
\text{det}(A') = - \text{det}(A)
\]
এখানে, \( A' \) হল সেই ম্যাট্রিক্স যেটির দুইটি সারি বা কলাম বিনিময় করা হয়েছে।
প্রমাণ:
ধরা যাক, \( A = \begin{bmatrix} a_1 & a_2 & \cdots & a_n \\ b_1 & b_2 & \cdots & b_n \\ \vdots & \vdots & \ddots & \vdots \\ z_1 & z_2 & \cdots & z_n \end{bmatrix} \) একটি \( n \times n \) ম্যাট্রিক্স।
যখন দুইটি সারি বিনিময় করা হয়, তখন নির্ণায়কের মানের সাইন পরিবর্তিত হয় (এটি একধরণের গাণিতিক প্রপার্টি)।
যদি কোনো সারি বা কলাম পুরোপুরি শূন্য থাকে, তবে সেই ম্যাট্রিক্সের নির্ণায়ক শূন্য হবে।
\[
\text{det}(A) = 0
\]
এখানে, \( A \) এমন একটি ম্যাট্রিক্স যার কোনো সারি বা কলাম সম্পূর্ণ শূন্য।
প্রমাণ:
ধরা যাক, \( A \) একটি \( n \times n \) ম্যাট্রিক্স যার কোনো সারি বা কলাম শূন্য। এতে, নির্ণায়ক হিসাব করার জন্য কোলামের বা সারির উপাদানগুলোর গুণফল শূন্য হবে, ফলে নির্ণায়ক শূন্য হবে।
যদি \( A \) একটি \( n \times n \) ম্যাট্রিক্স হয় এবং \( k \) একটি স্কেলার সংখ্যা হয়, তবে
\[
\text{det}(kA) = k^n \cdot \text{det}(A)
\]
প্রমাণ:
যখন \( A \) ম্যাট্রিক্সের সমস্ত উপাদানকে \( k \)-এর সাথে গুণ করা হয়, তখন গুণফলে \( k \) প্রতিটি সারি বা কলামের জন্য \( k \)-এর গুণফল হয়, ফলে নির্ণায়কের মান \( k^n \) এর গুণফলে পরিণত হয়।
যদি \( A \) একটি \( n \times n \) ম্যাট্রিক্স হয়, তবে তার ট্রান্সপোজ \( A^T \) এর নির্ণায়ক হবে \( A \)-এর নির্ণায়কের সমান। অর্থাৎ,
\[
\text{det}(A^T) = \text{det}(A)
\]
প্রমাণ:
ম্যাট্রিক্সের ট্রান্সপোজ করার ফলে সারি এবং কলামের স্থান পরিবর্তিত হয়, কিন্তু নির্ণায়ক পরিবর্তিত হয় না। তাই, \(\text{det}(A^T) = \text{det}(A)\) হয়।
যদি একটি ম্যাট্রিক্সের কোনো সারি বা কলাম অন্য একটি সারি বা কলামের গুণফল হয়, তবে ম্যাট্রিক্সের নির্ণায়ক শূন্য হবে।
প্রমাণ:
ধরা যাক, \( A \) একটি \( n \times n \) ম্যাট্রিক্স, এবং এর কোনো একটি সারি বা কলাম অন্য একটি সারি বা কলামের গুণফল। এতে, নির্ণায়কের মান শূন্য হবে কারণ ওই সারি বা কলামগুলোর মধ্যে কোনো ভিন্নতা নেই।
নির্ণায়কের এই গুণাবলী ম্যাট্রিক্সের বিশ্লেষণ এবং গাণিতিক সমীকরণের সমাধানে গুরুত্বপূর্ণ ভূমিকা পালন করে। এগুলো বিভিন্ন গণনাযুক্ত সিদ্ধান্ত এবং গাণিতিক নিয়মাবলী প্রমাণের জন্য ব্যবহার করা হয়।
ম্যাট্রিক্স হলো একটি গাণিতিক কাঠামো, যা সংখ্যার বা উপাদানের একটি আয়তক্ষেত্রাকার বা স্কয়ার বিন্যাস। এটি লিনিয়ার অ্যালজেব্রা, পরিসংখ্যান, গাণিতিক মডেলিং, এবং অন্যান্য গাণিতিক এবং প্রকৌশল সমস্যা সমাধানে ব্যবহৃত হয়।
একটি ম্যাট্রিক্স একটি \( m \times n \) আয়তক্ষেত্রাকার গাণিতিক কাঠামো, যার মধ্যে \( m \) সারি (rows) এবং \( n \) কলাম (columns) থাকে। প্রতিটি উপাদান একটি নির্দিষ্ট সারি ও কলামের交মিলনে থাকে।
এটি সাধারণত এর উপাদানগুলি \( a_{ij} \) দিয়ে প্রকাশ করা হয়, যেখানে \( i \) সারির সূচক এবং \( j \) কলামের সূচক।
যেমন একটি ৩x৩ ম্যাট্রিক্স \( A \) হবে:
\[
A = \begin{bmatrix}
a_{11} & a_{12} & a_{13} \
a_{21} & a_{22} & a_{23} \
a_{31} & a_{32} & a_{33}
\end{bmatrix}
\]
এখানে, \( a_{ij} \) ম্যাট্রিক্সের উপাদান, যেখানে \( i \) সারি এবং \( j \) কলামের সূচক।
ম্যাট্রিক্স গাণিতিক সমস্যা সমাধানে একটি অত্যন্ত গুরুত্বপূর্ণ উপাদান। এটি লিনিয়ার সমীকরণ সমাধান, গাণিতিক মডেলিং, পরিসংখ্যান, ডিজাইন অ্যানালিসিস, এবং অন্যান্য শাখায় ব্যাপকভাবে ব্যবহৃত হয়।
ম্যাট্রিক্সের অনেক মৌলিক গাণিতিক সূত্র রয়েছে, যা ম্যাট্রিক্সের অপারেশন ও বিভিন্ন গাণিতিক প্রয়োগে ব্যবহৃত হয়। এখানে কিছু গুরুত্বপূর্ণ সূত্র এবং তার প্রমাণ দেওয়া হলো:
সূত্র:
\[
A + B = B + A
\]
এখানে, \( A \) এবং \( B \) একই আকারের দুটি ম্যাট্রিক্স।
প্রমাণ:
যেহেতু ম্যাট্রিক্সের যোগফলে প্রতিটি উপাদান শুধুমাত্র ঐ দুইটি ম্যাট্রিক্সের সংশ্লিষ্ট উপাদানের যোগফল হয়, তাই,
\[
A + B = \begin{bmatrix} a_{ij} + b_{ij} \end{bmatrix}, \quad B + A = \begin{bmatrix} b_{ij} + a_{ij} \end{bmatrix}
\]
এবং যেহেতু \( a_{ij} + b_{ij} = b_{ij} + a_{ij} \), এটি কমিউটেটিভ প্রপার্টি।
সূত্র:
\[
A(BC) = (AB)C
\]
এখানে, \( A \), \( B \), এবং \( C \) হল ম্যাট্রিক্স, এবং \( AB \), \( BC \) তাদের গুণফল।
প্রমাণ:
ম্যাট্রিক্স গুণফলে প্রতিটি উপাদান কলাম এবং সারির গুণফল হয়। এই গুণফল কম্পিউট করার সময় অ্যাসোসিয়েটিভ প্রপার্টি ঠিকভাবে কাজ করে, কারণ গুণফলে প্রতিটি উপাদান পর্যায়ক্রমে গুণ হয়। তাই \( A(BC) = (AB)C \) হবে।
সূত্র:
\[
k(A + B) = kA + kB
\]
এখানে, \( A \) এবং \( B \) হল ম্যাট্রিক্স এবং \( k \) একটি স্কেলার সংখ্যা।
প্রমাণ:
ম্যাট্রিক্স \( A \) এবং \( B \)-এর উপাদানগুলো যখন স্কেলার \( k \)-এর সাথে গুণ করা হয়, তখন এটি হবে:
\[
k(A + B) = k \begin{bmatrix} a_{ij} + b_{ij} \end{bmatrix} = \begin{bmatrix} k(a_{ij} + b_{ij}) \end{bmatrix}
\]
এবং,
\[
kA + kB = \begin{bmatrix} k a_{ij} \end{bmatrix} + \begin{bmatrix} k b_{ij} \end{bmatrix} = \begin{bmatrix} k(a_{ij} + b_{ij}) \end{bmatrix}
\]
এটা সমান হবে। তাই, \( k(A + B) = kA + kB \) প্রমাণিত হলো।
সূত্র:
\[
k(AB) = (kA)B = A(kB)
\]
এখানে, \( A \), \( B \) ম্যাট্রিক্স এবং \( k \) একটি স্কেলার সংখ্যা।
প্রমাণ:
\( k \) স্কেলার সংখ্যাটি গুণফলের উপর বিতরণযোগ্য। অর্থাৎ, \( k \)-এর সাথে গুণফলে প্রতিটি উপাদানকে \( k \)-এর গুণফলে গুণ করা হয়। তাই,
\[
k(AB) = \begin{bmatrix} k \times (a_{ij} \times b_{ij}) \end{bmatrix}
\]
এবং,
\[
(kA)B = \begin{bmatrix} (k \times a_{ij}) \times b_{ij} \end{bmatrix}, \quad A(kB) = \begin{bmatrix} a_{ij} \times (k \times b_{ij}) \end{bmatrix}
\]
তাহলে, \( k(AB) = (kA)B = A(kB) \) প্রমাণিত হলো।
সূত্র:
\[
(AB)^T = B^T A^T
\]
এখানে, \( A \) এবং \( B \) ম্যাট্রিক্স।
প্রমাণ:
\( AB \)-এর ট্রান্সপোজ হবে:
\[
(AB)^T = \begin{bmatrix} (AB){ij} \end{bmatrix}^T = \begin{bmatrix} (AB){ji} \end{bmatrix}
\]
এবং,
\[
B^T A^T = \begin{bmatrix} B_{ij} \end{bmatrix}^T \begin{bmatrix} A_{ij} \end{bmatrix}^T = \begin{bmatrix} B_{ji} A_{ji} \end{bmatrix}
\]
তাহলে, \( (AB)^T = B^T A^T \) প্রমাণিত হলো।
সূত্র:
\[
A^{-1}A = I
\]
এখানে, \( A^{-1} \) হল \( A \)-এর ইনভার্স, এবং \( I \) হল ঐ ম্যাট্রিক্সের আইডেন্টিটি ম্যাট্রিক্স।
প্রমাণ:
যেহেতু \( A^{-1} \) হল \( A \)-এর ইনভার্স, এবং ইনভার্সের সংজ্ঞা অনুযায়ী,
\[
A^{-1}A = I
\]
এটি গাণিতিকভাবে সঠিক।
সূত্র:
\[
\text{det}(AB) = \text{det}(A) \times \text{det}(B)
\]
এখানে, \( A \) এবং \( B \) ম্যাট্রিক্স।
প্রমাণ:
ডিটারমিন্যান্টের গুণফলে এটি প্রমাণ করা যায় যে, যখন দুটি ম্যাট্রিক্সের গুণফল হবে, তাদের ডিটারমিন্যান্টের গুণফল হবে। এটি একটি সাধারণ গাণিতিক তত্ত্ব যা ম্যাট্রিক্সের উপাদানের উপর ভিত্তি করে কাজ করে।
এই গুণাবলীর সাহায্যে ম্যাট্রিক্সের বিভিন্ন গাণিতিক সমীকরণ এবং প্রয়োগ করা যায়। এগুলো লিনিয়ার অ্যালজেব্রা, সিস্টেম অফ লিনিয়ার ইকুয়েশন, এবং পরিসংখ্যান বা অন্যান্য গাণিতিক সমস্যা সমাধানে অত্যন্ত গুরুত্বপূর্ণ।
প্রাক্কলন পরিসংখ্যানের একটি গুরুত্বপূর্ণ অধ্যায় যা আমাদের অনুমান করতে সাহায্য করে যে, কোনো জনসংখ্যার নির্দিষ্ট বৈশিষ্ট্য কেমন হতে পারে। এটি বিভিন্ন বাস্তব সমস্যার সমাধান এবং সিদ্ধান্ত গ্রহণে গুরুত্বপূর্ণ ভূমিকা পালন করে।
প্রাক্কলন হলো একটি পদ্ধতি যার মাধ্যমে একটি ছোট নমুনার সাহায্যে জনসংখ্যার একটি বৈশিষ্ট্যের মান নির্ধারণ করা হয়।
এটি এমন একটি পদ্ধতি যেখানে জনসংখ্যার নির্দিষ্ট বৈশিষ্ট্যের একটি একক মান নির্ধারণ করা হয়।
গুণাবলি:
এটি এমন একটি পদ্ধতি যেখানে নির্দিষ্ট সীমার মধ্যে জনসংখ্যার বৈশিষ্ট্যের মান নির্ধারণ করা হয়।
গুণাবলি:
যে সমগ্র সেট থেকে নমুনা নেওয়া হয়।
জনসংখ্যার একটি ছোট অংশ যা পরিসংখ্যান বিশ্লেষণে ব্যবহৃত হয়।
নমুনার উপর ভিত্তি করে গাণিতিক হিসাব।
জনসংখ্যার বৈশিষ্ট্যের প্রকৃত মান।
প্রাক্কলনের নির্ভুলতা নির্ধারণে ব্যবহার করা হয়।
১. গড়ের ব্যবহার (Mean):
নমুনার গড় ব্যবহার করে প্রাক্কলন করা হয়।
\( \bar{x} = \frac{\Sigma x}{n} \)
২. মধ্যমার ব্যবহার (Median):
নমুনার মধ্যবর্তী মান ব্যবহার করা হয়।
উদাহরণ: নমুনা আয় \( [২০, ২২, ২৪, ২৬, ২৮] \), এখানে মধ্যমা \( ২৪ \)।
১. পূর্ববর্তী তথ্যের ব্যবহার।
২. পূর্ব অভিজ্ঞতার উপর ভিত্তি করে সিদ্ধান্ত।
দেশের জিডিপি, জনসংখ্যার প্রবৃদ্ধি বা গড় আয় প্রাক্কলনে ব্যবহৃত হয়।
নতুন পণ্যের চাহিদা নির্ধারণ, উৎপাদন পরিকল্পনা ইত্যাদিতে সাহায্য করে।
বিজ্ঞান ও প্রযুক্তিতে পরীক্ষার ফলাফলের প্রাক্কলন।
নমুনা আয় $২০,০০০, $২৫,০০০ এবং $২২,০০০।

নমুনার উপর ভিত্তি করে প্রাক্কলিত সীমা:
\( ১৫০ \text{ মিমি } - ২০০ \text{ মিমি} \)।
প্রাক্কলন হলো একটি কার্যকর পদ্ধতি যা পরিসংখ্যানের মাধ্যমে ভবিষ্যৎ বা অজানা মান সম্পর্কে ধারণা দেয়। এটি অর্থনীতি, ব্যবসা, গবেষণা এবং আরও অনেক ক্ষেত্রে সিদ্ধান্ত গ্রহণে সাহায্য করে।
পরিসংখ্যানে প্রাক্কলনের মাধ্যমে নমুনা থেকে জনসংখ্যার বৈশিষ্ট্য অনুমান করা হয়। প্রাক্কলনের পদ্ধতিগুলো মূলত দুই ধরনের: গাণিতিক পদ্ধতি এবং আনুমানিক পদ্ধতি।
গাণিতিক পদ্ধতিতে প্রাক্কলন করার জন্য নমুনা থেকে গণিত ও পরিসংখ্যানের বিভিন্ন সূত্র ব্যবহার করা হয়। এগুলোর মধ্যে উল্লেখযোগ্য হলো:
উদাহরণ:
যদি কোনো এলাকার নমুনা আয়ের মান হয় $২০,০০০, $২৫,০০০ এবং $২২,০০০, তবে গড়:
\[
\bar{x} = \frac{২০০০০ + ২৫০০০ + ২২০০০}{৩} = ২২,৩৩৩
\]
উদাহরণ:
নমুনা আয়: $১৮,০০০, $২০,০০০, $২২,০০০, $২৪,০০০, এবং $২৬,০০০।
মধ্যমা: $২২,০০০ (মধ্যবর্তী মান)।
উদাহরণ:
নমুনা: $১৫,০০০, $২০,০০০, $২০,০০০, $২৫,০০০।
মোড: $২০,০০০ (সবচেয়ে ঘন ঘন উপস্থিত)।
সূত্র:
\[
\bar{x} \pm Z \cdot \frac{s}{\sqrt{n}}
\]
যেখানে,
\( \bar{x} \) = নমুনার গড়
\( Z \) = নির্দিষ্ট বিশ্বাসযোগ্যতার স্তরের জন্য Z-স্কোর
\( s \) = নমুনার মান বিচ্যুতি
\( n \) = নমুনার সংখ্যা
আনুমানিক পদ্ধতি পূর্ব অভিজ্ঞতা এবং বাস্তবতার উপর ভিত্তি করে করা হয়।
নমুনা: $১০,০০০, $১২,০০০, $১৪,০০০।
গড়:

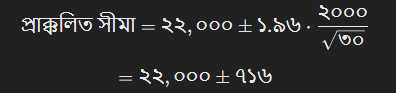
নমুনার গড়: $২২,০০০
বিশ্বাসযোগ্যতার স্তর: ৯৫%
\( Z = ১.৯৬, s = ২,০০০, n = ৩০ \)
সীমা: $২১,২৮৪ থেকে $২২,৭১৬।
প্রাক্কলন পদ্ধতিতে গাণিতিক এবং আনুমানিক উভয় পদ্ধতি ব্যবহার করা হয়। গাণিতিক পদ্ধতি অধিক নির্ভুল এবং পরিসংখ্যানের উপর ভিত্তি করে ফলাফল প্রদান করে, যেখানে আনুমানিক পদ্ধতি বাস্তব পরিস্থিতি ও অভিজ্ঞতার উপর নির্ভর করে।
প্রাক্কলনের ধর্মগুলো নির্ধারণ করে যে একটি প্রাক্কলন কতটা কার্যকর এবং সঠিক। কার্যকর প্রাক্কলন পদ্ধতিকে চিহ্নিত করতে নিম্নলিখিত ধর্মগুলো বিবেচনা করা হয়:
উদাহরণ:
যদি কোনো এলাকার গড় আয়ের প্রকৃত মান $২০,০০০ এবং প্রাক্কলিত গড় বারবার $২০,০০০ প্রদান করে, তবে এটি পক্ষপাতহীন।
উদাহরণ:
১০০ জনের নমুনার ভিত্তিতে গড় আয় $১৯,৮০০ এবং ১০০০ জনের নমুনার ভিত্তিতে গড় আয় $১৯,৯৫০, এটি সামঞ্জস্যপূর্ণ।
উদাহরণ:
দুইটি প্রাক্কলকের মধ্যে একটির বৈচিত্র্য ১০ এবং অপরটির বৈচিত্র্য ১৫। প্রথমটি বেশি কার্যকর।
উদাহরণ:
নমুনার প্রতিটি মান ব্যবহার করে গড় নির্ধারণ যথার্থ প্রাক্কলন।
প্রাক্কলনের ধর্মগুলো প্রমাণ করার জন্য গাণিতিক সূত্র এবং পরিসংখ্যানের বিভিন্ন নিয়ম ব্যবহার করা হয়। এখানে কয়েকটি গুরুত্বপূর্ণ প্রমাণ উল্লেখ করা হলো:
ধরা যাক, \( \hat{\theta} \) একটি প্রাক্কলক এবং জনসংখ্যার প্যারামিটার \( \theta \)।
পক্ষপাতহীনতার জন্য,
\[
E(\hat{\theta}) = \theta
\]
উদাহরণ: গড়ের ক্ষেত্রে,
\[
\hat{\mu} = \frac{\Sigma x}{n}
\]
এবং,
\[
E(\hat{\mu}) = \mu
\]
অতএব, গড় একটি পক্ষপাতহীন প্রাক্কলক।
ধরা যাক, \( \hat{\theta}n \) একটি প্রাক্কলক। সামঞ্জস্যতার জন্য,
\[
\lim{n \to \infty} P(|\hat{\theta}_n - \theta| < \epsilon) = 1
\]
অর্থাৎ, \( n \)-এর মান বাড়ালে প্রাক্কলক \( \theta \)-এর কাছাকাছি পৌঁছাবে।
ধরা যাক, \( \hat{\theta}_1 \) এবং \( \hat{\theta}_2 \) দুইটি প্রাক্কলক। যদি,
\[
Var(\hat{\theta}_1) < Var(\hat{\theta}_2)
\]
তাহলে, \( \hat{\theta}_1 \) বেশি কার্যকর।
উদাহরণ:
গড়ের প্রাক্কলনের জন্য,
\[
Var(\bar{x}) = \frac{\sigma^2}{n}
\]
এটি দেখায় যে নমুনার আকার বৃদ্ধির সঙ্গে গড়ের বৈচিত্র্য কমে যায়।
ধরা যাক, \( \hat{\theta} \) একটি যথার্থ প্রাক্কলক। এটি জনসংখ্যার সমস্ত প্রাসঙ্গিক তথ্য ধারণ করবে।
পরীক্ষার জন্য, যথার্থ প্রাক্কলক সর্বাধিক সম্ভাব্যতা (maximum likelihood) পদ্ধতি দিয়ে যাচাই করা হয়।
প্রাক্কলনের ধর্মগুলো কার্যকর এবং নির্ভুল প্রাক্কলন পদ্ধতি নির্ধারণে সাহায্য করে। পক্ষপাতহীনতা, সামঞ্জস্যতা, দক্ষতা, যথার্থতা এবং সহমিতি একটি প্রাক্কলন পদ্ধতির সঠিকতা প্রমাণ করে। এগুলোর গাণিতিক ভিত্তি এবং ব্যবহারিক প্রয়োগ নিশ্চিত করে যে প্রাক্কলন বাস্তব জীবনের সমস্যাগুলো সমাধানে কার্যকর।
অন্তর প্রাক্কলন হলো পরিসংখ্যানের এমন একটি পদ্ধতি যেখানে জনসংখ্যার কোনো নির্দিষ্ট বৈশিষ্ট্যের মান একটি সীমার (interval) মধ্যে নির্ধারণ করা হয়। এটি বিন্দু প্রাক্কলনের তুলনায় বেশি নির্ভুল এবং সঠিক কারণ এটি একটি সম্ভাব্য সীমার মধ্যে ফলাফল প্রদান করে।
সীমার নিচের মান, যা একটি প্রাক্কলনের সর্বনিম্ন সম্ভাব্য মান।
সীমার উপরের মান, যা একটি প্রাক্কলনের সর্বোচ্চ সম্ভাব্য মান।
সাধারণত ৯৫% বা ৯৯% ব্যবহার করা হয়।
প্রাক্কলিত সীমার মান নির্ধারণে যে পরিমাণ ত্রুটি থাকতে পারে।
যদি জনসংখ্যার মান বিচ্যুতি (standard deviation) জানা থাকে:
\[
\bar{x} \pm Z \cdot \frac{\sigma}{\sqrt{n}}
\]
যদি মান বিচ্যুতি অজানা থাকে:
\[
\bar{x} \pm t \cdot \frac{s}{\sqrt{n}}
\]
যেখানে:
ধরা যাক, একটি এলাকার নমুনার গড় আয় $৫০,০০০, জনসংখ্যার মান বিচ্যুতি \( \sigma = ৫,০০০ \), এবং নমুনার আকার \( n = ১০০ \)।
৯৫% বিশ্বাসযোগ্যতার স্তরে, \( Z = ১.৯৬ \)।
\[
\bar{x} \pm Z \cdot \frac{\sigma}{\sqrt{n}}
\]
\[
৫০,০০০ \pm ১.৯৬ \cdot \frac{৫,০০০}{\sqrt{১০০}}
\]
\[
৫০,০০০ \pm ১.৯৬ \cdot ৫০০ = ৫০,০০০ \pm ৯৮০
\]
অতএব, প্রাক্কলিত আয় $৪৯,০২০ থেকে $৫০,৯৮০ এর মধ্যে।
ধরা যাক, নমুনার গড় $২০০, নমুনার মান বিচ্যুতি \( s = ২০ \), নমুনার আকার \( n = ২৫ \), এবং ৯৫% বিশ্বাসযোগ্যতার স্তরে \( t = ২.০৬৪ \)।
\[
\bar{x} \pm t \cdot \frac{s}{\sqrt{n}}
\]
\[
২০০ \pm ২.০৬৪ \cdot \frac{২০}{\sqrt{২৫}}
\]
\[
২০০ \pm ২.০৬৪ \cdot ৪ = ২০০ \pm ৮.২৫৬
\]
অতএব, প্রাক্কলিত আয় $১৯১.৭৪৪ থেকে $২০৮.২৫৬ এর মধ্যে।
মুদ্রাস্ফীতি, গড় বেতন ইত্যাদির প্রাক্কলন।
নতুন পণ্যের চাহিদা নির্ধারণে ব্যবহৃত হয়।
পরীক্ষার ফলাফল বিশ্লেষণে ব্যবহার হয়।
রোগীর গড় বয়স বা ওজন প্রাক্কলনে।
অন্তর প্রাক্কলন হলো একটি নির্ভুল এবং কার্যকর পদ্ধতি যা নমুনার তথ্য ব্যবহার করে জনসংখ্যার বৈশিষ্ট্য নির্ধারণ করে। এটি ভবিষ্যৎ সিদ্ধান্ত গ্রহণ এবং পরিসংখ্যান বিশ্লেষণে গুরুত্বপূর্ণ ভূমিকা পালন করে।
Read more