আমরা চারপাশের যা কিছু আছে সেগুলো থেকে যখন আলো প্রতিফলিত হয়ে আমাদের চোখে এসে পড়ে আমরা তখন সেগুলো দেখতে পাই। আগের অধ্যায়ে শব্দকে ভরা হিসেবে জেনেছি, এই অধ্যায়ে আমরা আলোকে তরঙ্গ হিসেবে জানব, তবে সেটি হবে সম্পূর্ণ ভিন্ন এক ধরনের তরঙ্গ যার নাম বিদ্যুৎ চৌম্বকীয় তরঙ্গ।
আলো যখন সমতল আয়নায় প্রতিফলিত হয় তখন সেটি প্রতিবিম্ব তৈরি করে, আমরা সবাই সেই প্রতিবিম্বের সাথে পরিচিত। সমতল আয়না না হয়ে গোলাকৃতির আয়নাও ব্যবহার করা যায় তখন সেটি যে প্রতিবিম্ব তৈরি করবে সেটি হবে অন্যরকম। এই অধ্যায়ে আমরা নানা ধরনের আয়নার নানা ধরনের প্রতিবিম্বের বিষয়গুলোও আলোচনা করব।
আমরা চোখে যেটা দেখতে পাই, সেটা হচ্ছে আলো। আমরা চোখে গাছপালা দেখি, আকাশ দেখি, চেয়ার-টেবিল দেখি, মানুষ দেখি, তার মানে এই নয় যে পাছপালা, আকাশ, চেয়ার-টেবিল কিংবা মানুষ হচ্ছে আলো। এগুলো থেকে আলো প্রতিফলিত হয়ে সেই আলোটা আমাদের চোখে পড়ে, চোখের রেটিনা থেকে সেই আলো দিয়ে তৈরি সংকেত আমাদের মস্তিষ্কে পৌঁছায় আর আমাদের মস্তিক্ষ বুঝতে পাৱে কোনটা গাছপালা কিংবা কোনটা মানুষ। পুরো ব্যাপারটা শুরু হয় চোখের মাঝে আলো ঢোকা থেকে।
আলো হচ্ছে বিদ্যুৎ চৌম্বকীয় তরঙ্গ। তরঙ্গ হলেই তার একটা তরঙ্গ দৈর্ঘ্য থাকে, তার মানে আলোরও নিশ্চয়ই তরঙ্গ দৈর্ঘ্য আছে। আমরা যারা পুকুরে ঢিল ছুড়ে কিংবা একটা দড়িতে ঝাঁকুনি দিয়ে তরঙ্গ তৈরি করেছি, তারা জানি যে ইচ্ছে করলেই ছোট-বড় তরঙ্গ দৈর্ঘ্যের ভরা তৈরি করা যায়, তাই আলোরও নিশ্চয়ই নানা তরঙ্গ দৈর্ঘ্য থাকতে পারে। কথাটা সঠিক, বিদ্যুৎ চৌম্বকীয় তরঙ্গের দৈর্ঘ্য যা কিছু হতে পারে। সেটা কয়েক কিলোমিটার থেকেও বেশি হতে পারে আবার এক মিটারের ট্রিলিয়ন মিলিয়ন ভাগের এক ভাগও হতে পারে। যে বিষয়টা আমাদের ভালো করে জানা দরকার, সেটি হচ্ছে এই সম্ভাব্য বিশাল তরঙ্গ দৈর্ঘ্যের ছোট একটা অংশ আমরা দেখতে পাই, তরঙ্গ দৈর্ঘ্য এর থেকে বেশি হলেও আমরা দেখতে পাই না আবার এর থেকে ছোট হলেও আমরা দেখতে পাই না। তরঙ্গ দৈর্ঘ্য 400 nm থেকে 700 nm এর ভেতরে হলে আমরা বিদ্যুৎ চৌম্বকীয় তরঙ্গ দেখতে পাই এবং সেটাকে আমরা বলি আলো। আমরা যে চোখে নানা রং দেখতে পাই সেগুলোও আসলে বিভিন্ন তরঙ্গ দৈর্ঘ্যের আলো। তরঙ্গ দৈর্ঘ্য যখন ছোট হয় সেটা হয় বেগুনি। যখন তরঙ্গ দৈর্ঘ্য বাড়তে থাকে তখন সেটা নীল সবুজ হলুদ কমলা লাল হয়ে চোখের কাছে অদৃশ্য হয়ে যায়। মানুষের চোখ এই ব্যাপ্তির বাইরে তরঙ্গ দৈর্ঘ্য দেখতে পায় না কিন্তু পোকামাকড় বা অন্য অনেক প্রাণী এর বাইরেও দেখতে পায়। বিভিন্ন আলোতে মানুষের চোখের সংবেদনশীলতা 8.01 চিত্রতে দেখানো হয়েছে।
(8.01) চিত্রে আলোর বিভিন্ন তরঙ্গ দৈর্ঘের যদি দৃশ্যমান আলোর সবচেয়ে ছোট তরঙ্গ দৈর্ঘ্য থেকেও ছোট হয়, সেটাকে আমরা বলি আলট্রা ভায়োলেট আলো, আরো ছোট হলে এক্স-রে আরো ছোট হলে গামা রে—যেটা তেজস্ক্রিয় নিউক্লিয়াস থেকে বের হয়। আবার তরঙ্গ দৈর্ঘ্য যদি দৃশ্যমান আলোর সবচেয়ে বড় তরঙ্গ দৈর্ঘ্য থেকেও বড় হয়, সেটাকে আমরা বলি ইনফ্রারেড, আরো বড় হলে মাইক্রোওয়েভ, আরো বড় হলে রেডিও ওয়েভ। পদার্থবিজ্ঞান শিখতে হলে যে বিষয়গুলো জানতে হয়, বিদ্যুৎ চৌম্বকীয় তরঙ্গের এই বিভাজনটি হচ্ছে তার সবচেয়ে গুরুত্বপূর্ণ একটা বিষয়।
প্রতিফলন কথাটা বলতেই আমাদের প্রায় সবার চোখেই আয়নার সামনে দাঁড়িয়ে থাকার চিত্রটা ভেসে ওঠে কিন্তু মনে রাখতে হবে প্রতিফলন বিষয়টা আরো অনেক ব্যাপক। যখনই এক মাধ্যম থেকে অন্য মাধ্যমে আলোকে পাঠানো হয়, তখনই আসলে তিনটি ভিন্ন ভিন্ন ঘটনা ঘটে, তার একটি হচ্ছে প্রতিফলন। অন্য দুটি হচ্ছে প্রতিসরণ আর শোষণ।
প্রথম মাধ্যম থেকে দ্বিতীয় মাধ্যমে যাবার সময় খানিকটা আলো আবার প্রথম মাধ্যমেই ফিরে আসে সেটার নাম হচ্ছে প্রতিফলন। খানিকটা আলো দ্বিতীয় মাধ্যমে ঢুকে যেতে পারে সেটা হচ্ছে প্রতিসরণ। আবার খানিকটা আলো শোষিত হয়ে যায় সেটার নাম হচ্ছে শোষণ। এই অধ্যায়ে আমরা প্রতিফলন এবং পরের অধ্যারে প্রতিসরণ নিয়ে আলোচনা করব।
আগেই বলা হয়েছে আলো এক ধরনের তরঙ্গ, সাধারণভাবে তরঙ্গের যাওয়ার জন্য মাধ্যমের প্রয়োজন হয়, (পানি না থাকলে পানির ঢেউটা হবে কোথায়?) কিন্তু আলোর বিষয়টা সম্পূর্ণ ভিন্ন, এটা যেহেতু বিদ্যুৎ এবং চৌম্বক ক্ষেত্রের তরঙ্গ, তাই এটার জন্য কোনো মাধ্যমের দরকার নেই, আলো তার বিদ্যুৎ আর চৌম্বক ক্ষেত্র দুটির তরঙ্গ তৈরি করে নিজেরাই চলে যেতে পারে। কাজেই প্রতিফলন বা প্রতিসরণ ব্যাখ্যা করার জন্য যখন প্রথম এবং দ্বিতীয় মাধ্যমের কথা বলা হয়েছে, তখন একটি মাধ্যম আসলে শূন্য মাধ্যমও হতে পারত। সত্যি কথা বলতে কি আমাদের দৈনন্দিন জীবনে আমরা কাচ বা পানিতে আলোর প্রতিফলন এবং প্রতিসরণের যে উদাহরণগুলো দেখি সেখানে একটা মাধ্যম বাতাস অন্যটি কাচ (কিংবা পানি)। বাতাস এত হালকা মাধ্যম যে সেটাকে শূন্য মাধ্যম ধরে নিলে এমন কিছু বড় ভুল হয় না।
প্রতিফলনের সূত্র বোঝার আগে আমাদের কয়েকটা বিষয়কে সংজ্ঞায়িত করে নেওয়া দরকার। যখন এক মাধ্যম থেকে অন্য মাধ্যমে আলো এসে পড়ে আমরা আপাতত ধরে নিই সেটি হচ্ছে একটা সমতল। বিষয়টি বোঝার জন্য আমরা ধরে নিই যে আলোটা প্রতিফলিত হবে, সেটা একটা আলোক রেখা বা আলোক রশ্মি। যখন একটা আলোক রশ্মি এক মাধ্যম থেকে অন্য মাধ্যমের ওপর একটা বিন্দুতে এসে পড়ে প্রথমেই সেই বিন্দু থেকে একটা সম্ব কল্পনা করে নিতে হবে। যে আলোক রশ্মিটি এসে সেই বিন্দুটিতে পড়েছে এবং যে লম্বটি কল্পনা করেছ সেই দুটি রেখাকে নিয়ে একটি সমতল কল্পনা করে নাও। (চিত্র 8.02)
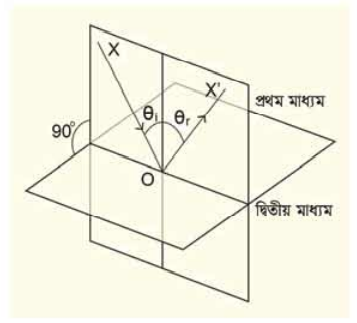
চিত্র 8.02:প্রথম মাধ্যম থেকে দ্বিতীয় মাধ্যমে আলোর প্রতিফলন
যে রশ্মিটি প্রথম মাধ্যম থেকে দ্বিতীয় মাধ্যমে ঢোকার জন্ম একটা বিষ্ণুতে আপতিত হয়েছে আমরা সেটাকে বলব, আপাতন রশ্মি (XO) । যে রশ্মিটি প্রতিফলিত হয়েছে (OX') সেটা হচ্ছে প্রতিফলিত র (বোঝাই যাচ্ছে যেটা দ্বিতীয় মাধ্যমে ঢুকে যাবে সেটা প্রতিসরিত রশ্মি—এই অধ্যায়ে সেটা নিয়ে আমরা আলোচনা করব না । ) আপতিত রশ্মি লম্বের সাথে যে কোণ করবে, সেটাকে বলব আপাতন কোণ (θi), প্রতিফলিত রশ্মি লম্বের সাথে যে কোণ (θr) করবে, সেটাকে বলব প্রতিফলন কোণ। এখন আমরা প্রতিফলনের সূত্র দুটি বলতে পারি
প্রথম সুত্র: আপাতন রশ্মি এবং লম্ব দিয়ে আমরা যে সমতলটি কল্পনা করে নিয়েছিলাম প্রতিফলিত রশ্মিটি সেই সমতলেই থাকবে।
দ্বিতীয় সূত্র: প্রতিফলন কোণটি হবে আপাতন কোণের সমান ।
প্রতিফলনের দুটি সূত্র বলা হলেই প্রতিফলন নিয়ে সবকিছু বলা হয়ে যায় না, সত্যি কথা বলতে কি প্রতিফলনের সবচেয়ে গুরুত্বপূর্ণ বিষয়টাই বলা হয়নি, কতটুকু প্রতিফলন হবে? প্রতিফলনের জন্য যদি আয়না ব্যবহার করা হয় তাহলে প্রায় পুরোটাই প্রতিফলিত হয়, কিন্তু প্রতিফলন কথাটি তো শুধু আয়নার জন্য তৈরি করা হয়নি—এটা তো যেকোনো দুটো মাধ্যমের মাঝে হতে পারে। কতটুকু প্রতিফলন হবে সেটার জন্য সূত্রটির নাম ফ্রেনেলের (Fresnel) সূত্র। সূত্রটা তোমরা আরেকটু বড় হয়ে শিখবে, এখন এটার মূল বিষয়টা জেনে শুধু রাখো— আপাতন কোণ যত বেশি হবে প্রতিফলনও হবে তত বেশি । তোমরা দেখেছ সাধারণ এক টুকরো কাচে প্রতিফলন হয় কম, মাত্র 4% থেকে 5%, বাকিটা ভেতরে দিয়ে প্রতিসরিত হয়ে যায়। কিন্তু প্রতিফলন কোণ যদি বেশি হয় 80° কিংবা 90° এর কাছাকাছি, তাহলে প্রতিফলিত আলো অনেক বেশি বেড়ে যায়। জানালার কাচের পাশে দাঁড়িয়ে তোমরা এখনই সেটা পরীক্ষা করে দেখতে পারো।
আমাদের চারপাশের জগতের সৌন্দর্যের বড় একটা অংশ আসে বিভিন্ন রং থেকে। কিন্তু রংটি আসে কেমন করে? আমরা যখন সবুজ পাতার মাঝে একটা লাল গোলাপ ফুল দেখি, সেটি কেন লাল কিংবা তার পাতাটি কেন সবুজ? বিষয়টা আরো বিস্ময়কর মনে হতে পারে যখন তোমরা দেখবে সবুজ আলোতে লাল ফুলটাকেই দেখাবে কুচকুচে কালো কিংবা লাল আলোতে সবুজ পাতাকে দেখাবে কুচকুচে কালো।
বিষয়টা আসলে সহজ, সাধারণ আলোতে (অনেক সময় বলে সাদা আলো),আসলে সবগুলো তরঙ্গ দৈর্ঘ্যই থাকে, রং যেহেতু তরঙ্গ দৈর্ঘ্যের ওপর নির্ভর করে, তাই বলা যেতে পারে সেখানে সব রঙের আলো রয়েছে। যখন সবগুলো রং থাকে তখন সেখানে আলাদাভাবে কোনো রং দেখা যায় না—তখন আলোটাকে আমরা বলি বর্ণহীন কিংবা সাদা আলো। এই আলোটা যখন একটা লাল গোলাপ ফুলে পড়ে তখন গোলাপ ফুলটা লাল রং ছাড়া অন্য সবগুলো রং শোষণ করে নেয়—তাই যে আলোটা প্রতিফলিত হয়ে আমাদের চোখে পড়ে, না এবং গোলাপ ফুলটাকে মনে হয় সাল। ঠিক সে রকম সবুজ পাতাটাতে সব রং এসে পড়ে এবং পাতাটা সবুজ ছাড়া অন্য সব রং শোষণ করে নেয়, তখন যে রংটা প্রতিফলিত হয় সেটাতে সবুজ ছাড়া অন্য কোনো রঙের আলো থাকে না বলে পাতাটাকে দেখায় সবুজ।
যদি সম্পূর্ণ লাল আলোতে এই গোলাপ ফুল এবং পাতাটাকে দেখা হতো তাহলে ফুলটাকে ঠিকই লাল দেখা যেত কারণ এটা লাল রং শোষণ করে না কিন্তু পাতাটাকে তার সঠিক রঙে না দেখিয়ে দেখাবে কালো। কারণ পাতাটা লাল রংকে শোষণ করে ফেলবে এবং কোনো রং প্রতিফলিত করবে না। ঠিক একই কারণে সবুজ আলোতে পাতাটা সবুজ দেখালেও সেই রংটা গোলাপ ফুল পুরোপুরি শোষণ করে নেবে বলে গোলাপ ফুল থেকে প্রতিফলিত হবার মতো কোনো রং থাকবে না বলে সেটাকে দেখাবে কালো ।
আয়না কিংবা আয়নার মতো মসৃণ পৃষ্ঠে আলোর সমান্তরাল রশ্মিগুলো প্রতিফলনের পরেও সমান্তরাল থাকে, কারণ প্রত্যেকটা রশ্মিই প্রতিফলনের সূত্র মেনে আপাতন কোণের সমান প্রতিফলন কোণে প্রতিফলিত হয়। পৃষ্ঠটি যদি মসৃণ না হয় তাহলেও প্রত্যেকটা রশ্মিই প্রতিফলনের সূত্র মেনে চলে কিন্তু একেক অংশের পৃষ্ঠ একেক কোণে থাকে বলে প্রতিফলনের পর আলোক রশ্মিগুলো ভিন্ন ভিন্ন কোণে প্রতিফলিত হয়। তখন প্রতিফলনের পর আর আলোক রশ্মিগুলো সমান্তরাল না থেকে চারদিকে ছড়িয়ে পড়ে। (চিত্র 8.03)এ ধরনের প্রতিফলনকে অনেক সময় ব্যান্ড প্রতিফলন বলা হয়।
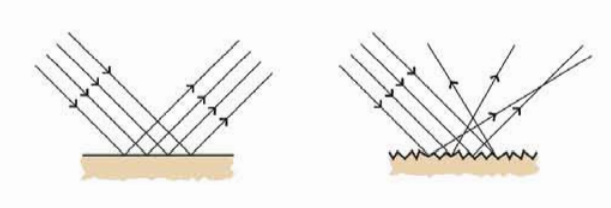
চিত্র 8.03:মসৃণ পৃষ্ঠে আলো প্রতিফলিত হয় কিন্তু অমসৃণ পৃষ্ঠে আলো বিচ্ছুরিত হয়।
আমরা সবাই আয়না (দর্পণ) দেখেছি। আয়নায় নিয়মিত প্রতিফলনের কারণে স্পষ্ট প্রতিবিম্বের তৈরি হয়। আয়না তৈরি করার জন্য কাচের পেছনে প্রতিফলনের উপযোগী রূপার প্রলেপ দেওয়া হয়। কাচের সামনের পৃষ্ঠ থেকে 4% আলো প্রতিফলিত হলেও পেছনের পৃষ্ঠ থেকে পুরো আলো প্রতিফলিত হয় বলে সেটি মূল প্রতিবিম্বটি তৈরি করে। টেলিস্কোপ বা অন্য অপটিক্যাল (Optical) যে যখন মূল প্রতিবিম্বটি খুব গুরুত্বপূর্ণ হয় তখন কাচের উপরেই রুপা বা অ্যালুমিনিয়ামের প্রলেপ দেওয়া হয় যেন একটি 4% হালকা আরেকটি 96% স্পষ্ট, এ রকম দুটি প্রতিবিম্ব তৈরি না হয়ে একটা 100% স্পষ্ট প্রতিবিম্ব তৈরি হয়।
তুমি যখন আয়নার সামনে দাঁড়াও তখন তুমি নিজের প্রতিবিম্ব দেখতে পাও, তুমি আয়নার যতটুকু সামনে আছ, তোমার মনে হবে প্রতিবিম্বটি বুঝি ঠিক ততটুকু পেছনে আছে।8.04 চিত্রে দেখানো হয়েছে X হচ্ছে একটি বস্তু সেখান থেকে তিনটি রশ্মি AB আয়নায় প্রতিফলিত হয়েছে (অর্থাৎ আপাতন কোণ = প্রতিফলিত কোণ)। প্রতিফলিত রশ্মিগুলোকে আমরা যদি আয়নার পেছনে বাড়িয়ে দিই তাহলে মনে হবে সবগুলো X' এক বিন্দুতে কেন্দ্রীভূত হয়েছে। এই বিন্দুটিই হচ্ছে X কস্তুটির প্রতিবিম্ব। সত্যিকার বস্তুতে একটা বিন্দু না থেকে অনেকগুলো বিন্দু থাকে এবং প্রতিটা বিন্দুর একটা করে প্রতিবিম্ব হয়ে পুরো বস্তুটির প্রতিবিম্ব তৈরি হয়।
আমরা যদি জ্যামিতি ব্যবহার করে প্রতিবিম্বটির অবস্থান দেখাতে চাই তাহলে কমপক্ষে দুটি রশ্মি আঁকতে হবে। চিত্রটা আঁকা অনেক সহজ হয় যদি আমরা সোজা লম্বভাবে যাওয়া রশ্মিটিকে (XP ) একটি রশ্মি হিসেবে নিই এবং চিত্রে যেভাবে দেখানো হয়েছে সেভাবে তার সাথে অন্য যেকোনো একটা রশ্মিকে (XO) নিই। OPX এবং OPX' ত্রিভুজ দুটি সর্বসম। অর্থাৎ XP - X'P তার মানে x বিন্দুর X' প্রতিবিম্বটি আয়না থেকে কন্তুটির সমান দূরত্বে তৈরি হয়েছে।
কোনো আয়নায় আমরা যদি একটি বস্তুর প্রতিবিম্ব দেখি সেটিকে যথেষ্ট বাস্তব মনে হলেও আসলে সেটি বাস্তব নয়। কারণ যেখান থেকে আলো আসছে বলে মনে হয় সেখান থেকে কোনো আলো আসছে না। আমরা পরে দেখব অনেক সময় কিন্তু সত্যি সত্যি এমনভাবে একটা প্রতিবিম্ব তৈরি হয়, যেখানে সত্যি সত্যি আলো কেন্দ্রীভূত হয় এবং সেখান থেকে আলোক রশ্মি বের হয়ে আসে। এ রকম প্রতিবিম্বকে বলে বাস্তব প্রতিবিম্ব এবং এই ধরনের প্রতিবিম্ব দিয়ে অনেক কাজ করা সম্ভব। আয়নায় যে প্রতিবিম্ব তৈরি হয়, সেখানে সত্যিকারের আলো কেন্দ্রীভূত হয় না, তাই এর নাম অবাস্তব প্রতিবিম্ব।
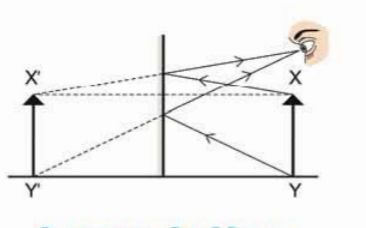
চিত্র 8.10: XY বস্তুটির প্রতিবিম্ব XY'
8.10 চিত্রে একটি মাত্র বিন্দু না হয়ে একটা বিস্তৃত বস্তুর প্রতিবিম্ব তৈরির হয় ক্ষেত্রে বস্তুর যেকোনো দুইটি বিন্দু X এবং Y থেকে আলো আয়নায় প্রতিফলিত হয়ে যথাক্রমে X' এবং Y' এ অবাস্তব প্রতিবিম্ব তৈরি করেছে অর্থাৎ মনে হচ্ছে চোখে আলোক রশ্মি আসছে X এবং Y থেকে। দেখাই যাচ্ছে XY এর যে দৈর্ঘ্য XY' এর সেই একই দৈর্ঘ্য। XY তে তীরের মাথাটি যদি উপরের দিকে হয় তাহলে X'Y' তেও তীরের মাথাটি উপরের দিকে হবে। অর্থাৎ সাধারণ আয়নায় কিংবা দর্পণে প্রতিবিম্ব:
(a) আয়না থেকে সমদূরত্বে
(b) অবাস্তব
(c) সোজা এবং
(d) সমান দৈর্ঘ্যের
আমরা আলাদা আলাদাভাবে এই বিষয়গুলো মনে করিয়ে দিচ্ছি কারণ একটু পরেই দেখব সাধারণ আয়নার বদলে অন্য ধরনের আয়না ব্যবহার করলে প্রতিবিম্ব ভিন্ন দুরত্বে হতে পারে, বাস্তব হতে পারে, উল্টো হতে পারে এমনকি ছোট কিংবা বড়ও হতে পারে।
সাধারণ সমতল আয়না আমরা সবাই দেখেছি কিন্তু সত্যিকারের গোলীয় আয়না আমরা সবাই নাও দেখতে পারি—তবে গোলীয় আয়নার মূল বিষয়টি কিন্তু চকচকে নতুন চামচে অনেকটা দেখা যায়। গোলীয় আয়না দুই রকমের হয়ে থাকে—অবতল এবং উত্তল। একটা ফাঁপা গোলকের খানিকটা কেটে তার পৃষ্ঠে রূপা বা অ্যালুমিনিয়ামের প্রলেপ লাগিয়ে অবতল কিংবা উত্তল গোলীয় আয়না তৈরি করা যায়। কোন পৃষ্ঠে ৰুপা বা অ্যালুমিনিয়ামের প্রলেপ দেওয়া হবে তার ওপর নির্ভর করবে এই গোলীয় আয়নাটি অবতল না উত্তল গোলীয় আয়না হবে।
তোমরা যদি কখনো একটা চকচকে চামচের নিচের বা পেছনের অংশে নিজের চেহারা দেখার চেষ্টা করে থাকো তাহলে নিশ্চয়ই লক্ষ করেছ যে সেখানে তুমি তোমার চেহারাটা সোজা দেখালেও সেটি হবে তুলনামূলকভাবে ছোট। চামচের এই অংশটা উত্তল আয়নার মতো কাজ করে। সত্যিকারের উত্তল আয়না একটা প্রকৃত গোলকের অংশ হয়। ধরা যাক, গোলকটির ব্যাসার্ধ r এবং তার একটা অংশ কেটে তার উত্তল অংশটির দিক থেকে আলোর প্রতিফলনের ব্যবস্থা করা হয়েছে। এই আয়নায় একটা সমান্তরাল আলো ফেলা হলে আলোটি চারদিকে ছড়িয়ে যাবে, ছড়িয়ে যাওয়া আলোক রশ্মিগুলো যদি আয়নার কেন্দ্রের দিকে বর্ধিত করি তাহলে মনে হবে সেটা বুঝি একটা বিন্দু থেকে ছড়িয়ে গেছে। ঐ বিন্দুটিকে বলে ফোকাস বিন্দু। উত্তল আয়নার যে পৃষ্ঠ থেকে প্রতিফলন হয় তার কেন্দ্রবিন্দুটিকে বলে মেরু বিন্দু এবং এই বিন্দু থেকে ফোকাস বিন্দুর দূরত্বটিকে বলে ফোকাস দূরত্ব (f)।
একটা গোলীয় আয়নাকে আমরা সব সময়ই একটা গোলকের অংশ হিসেবে কল্পনা করতে পারি। ঐ গোলকটির ব্যাসার্ধ যদি r হয় তাহলে ফোকাস দূরত্ব হবে r/2 |
আমরা আগেই বলেছি চামচের বাইরের অংশটা গোলীয় উত্তল আয়নার মতো কাজ করে এবং সেখানে তুমি নিজেকে দেখতে চাইলে ছোট এবং সোজা একটা প্রতিবিম্ব দেখতে পাও। যার অর্থ আমরা গোলীয় উত্তল আয়নার প্রতিবিম্বটি সব সময়ই ছোট দেখার কথা গোলীয় উত্তল আয়নায় কীভাবে প্রতিবিম্ব তৈরি হয় সেটি বোঝার জন্য আলোক রশ্মি গোলীয় উত্তল আয়নায় কীভাবে প্রতিফলিত হয় সেটি জানতে হবে। সেটি নির্ভর করে আলোক রশ্মি কী কোণে গোলীয় উত্তল আয়নায় এসে পড়ছে তার উপর। আমরা তিনটি বিশেষ আলোক রশ্মির প্রতিফলনের নিয়ম জানলেই কীভাবে প্রতিবিম্ব তৈরি হয় সেটি ব্যাখ্যা করতে পারব:
(i) আলোক রশ্মি কেন্দ্রমুখী হলে সেটি লম্বভাবে প্রতিফলিত হয়ে যেদিক থেকে এসেছে ঠিক সেদিকেই ফিরে যায়।
(ii) প্রধান অক্ষের সমান্তরাল রশ্মিটি প্রতিফলনের পর মনে হবে যেন রশ্মিটি ফোকাস বিন্দু থেকে ছড়িয়ে যাচ্ছে।
(iii) আলোক রশ্মির দিক পরিবর্তন করা হলে এটি যেদিক থেকে এসেছে ঠিক সেদিক দিয়ে ফিরে যায়। কাজেই কোনো আলোক রশ্মি ফোকাস অভিমুখী হলে সেটি প্রধান অক্ষের সাথে সমান্তরাল হয়ে প্রতিফলিত হবে।
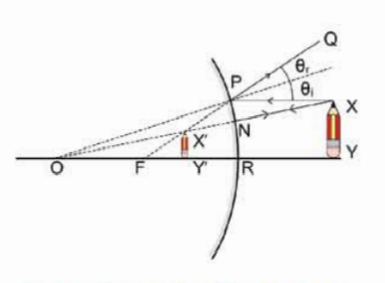
চিত্র 8.06: উত্তল আয়নায় একটি বস্তু XY ফোকাস দূরত্বের ভেতরে রাখা হলে প্রতিবিম্ব X'Y' ছোট দেখায়
আমরা এখন এই তিনটি নিয়ম ব্যবহার করে প্রতিবিম্ব তৈরি করতে পারব।8.06 চিত্রে একটা উত্তল আয়নার সামনে XY একটি বস্তু রাখা আছে Y বিন্দু থেকে আলো R বিন্দুতে এলে সেটি লম্বভাবে প্রতিফলিত হয়ে আবার Y বিন্দুর দিকেই ফিরে যায়, যার অর্থ XY বস্তুর Y বিন্দুর প্রতিবিম্বটি এই YO রেখার কোথাও হবে। সেটি ঠিক কোথায় জানতে হলে X বিন্দু থেকে অন্যদিকে আরেকটি রশ্মি আঁকতে হবে, আমাদের সেটি করার প্রয়োজন নেই কারণ X বিন্দুটির প্রতিবিম্বটি বের করে সেখান থেকে আমরা এটি জেনে নেব। x বিদুর প্রতিবিম্ব বের করার জন্য দুটি রশ্মি আঁকতে হবে, একটি আগের মতো সরাসরি বিন্দুর সাথে যুক্ত করি। YR রশ্মিটি যে রকম লম্বভাবে প্রতিফলিত হয়ে Y এর দিকে ফিরে গিয়েছিল এই রশ্মিটিও ঠিক একইভাবে N বিন্দুতে প্রতিফলিত হয়ে x এর দিকে ফিরে যাবে। দ্বিতীয় রশ্মিটি YR এর সাথে সমান্তরালভাবে আঁকা যেতে পারে, সেটা উত্তল আয়নার P বিন্দুতে স্পর্শ করলে মনে হবে যেন F বিন্দু থেকে ছড়িয়ে যাচ্ছে কাজেই আমরা FP কে যুক্ত করে Q এর দিকে বাড়িয়ে দিতে পারি। FP রেখাটা OX রেখাকে X' বিন্দুতে ছেদ করেছে, যার অর্থ X বিন্দুর প্রতিবিম্বটি হবে X' বিন্দুতে। X' থেকে OY রেখার ওপর লম্ব টানলে সেটা Y' বিন্দুতে ছেদ করবে। যেহেতু আমাদের মনে হবে X বিন্দুর প্রতিফলনটি আসছে X' বিন্দু থেকে সে কারণে আমাদের মনে হবে Y বিন্দুর প্রতিকলনটি আসছে Y' বিন্দু থেকে। কাজেই X'Y' হবে XY এর প্রতিবিম্ব।
দেখাই যাচ্ছে X'Y' সব সময় XY থেকে ছোট এবং XY উত্তল আয়না থেকে যত দূরে থাকবে XY হবে তত ছোট। প্রতিফলনের নিয়ম ব্যবহার করে উত্তল কিংবা অবতল আয়নায় প্রতিবিম্ব আঁকার এই পদ্ধতিটি ভালো করে জেনে রাখা দরকার, এটি পদার্থবিজ্ঞানের খুব প্রয়োজনীয় একটা পদ্ধতি।
বোঝাই যাচ্ছে X'Y' থেকে আসলে সত্যিকারের আলো বিচ্ছুরিত হচ্ছে না, আমাদের শুধু মনে হচ্ছে বুঝি প্রতিবিম্বটি এখানে আছে। কাজেই এটা অবাস্তব প্রতিবিম্ব। সাধারণ আয়নার প্রতিবিম্বের সাথে তুলনা করে আমরা বলতে পারি
(a) এই প্রতিবিম্বটির অবস্থান হবে ফোকাস বিন্দু এবং মেরু বিন্দুর মাঝখানে। বস্তুটি যত দূরে থাকবে প্রতিবিম্বটি ফোকাস বিন্দুর তত কাছে তৈরি হবে।
(b) এই প্রতিবিম্বটি অবাস্তব
(c) এটি সোজা
(d) এটা ছোট, বস্তুটি আয়না থেকে যত দূরে যাবে প্রতিবিম্বটি তত ছোট হতে থাকবে।
একটা চকচকে চামচের ভেতরের অংশটা অতল গোলীয় আয়নার উদাহরণ হতে পারে। তোমরা যারা চামচের ভেতরের দিকে তাকিয়েছ তারা নিশ্চয়ই লক্ষ করেছ সেখানে তোমার প্রতিবিম্বটি ছোট এবং সবচেৱে চমকপ্রদ হচ্ছে যে প্রতিবিম্বটি উল্টো। তোমরা চাইলে তোমার আঙুল চামচটার খুব কাছে এনে দেখতে পারো, তখন দেখবে আঙুলটা সোজাই দেখাচ্ছে। এবারে আস্তে আস্তে দূরে সরাতে থাক, দেখবে তোমার আঙুলটা বড় দেখাতে শুরু করেছে (আমরা সমতল আয়না কিংবা উত্তল আয়নায় এর আগে প্রতিবিম্ব তৈরি করতে পেরেছি কিন্তু কখনোই বস্তুর প্রকৃত আকার থেকে বড় প্রতিবিম্ব তৈরি করতে পারিনি—এই প্রথম বড় প্রতিবিম্ব দেখতে পাচ্ছি। আঙুলটা যদি আস্তে আস্তে সরাতে থাকো একসময় অবাক হয়ে দেখবে আঙুলের প্রতিবিম্বটা উল্টো হয়ে গেছে। এটাকে এখন যতই সরিরে নাও, এটা এখন সব সময় উল্টোই থেকে যাবে। (সমতল আয়না কিংবা উত্তল আয়না দিয়ে আমরা এর আগে কখনোই উল্টো প্রতিবিম্ব তৈরি করতে পারিনি—এই প্রথম আমরা উল্টো প্রতিবিম্ব দেখছি। )
কাজেই দেখতে পাচ্ছ চামচের বাইরের অংশটা উত্তল আয়নার মতো এবং ভেতরের অংশটা অবতল আয়নার মতো কাজ করে। সত্যিকারের অবতল আয়না আসলে একটা গোলকের অংশ। উত্তল আয়নার বেলায় বাইরের উত্তল অংশ থেকে আলো প্রতিফলিত হতো, অবতল আয়নার বেলায় আলো ভেতরের অবতল অংশ থেকে প্রতিফলিত হবে।
একটি অবতল আয়নায় সমান্তরাল আলো ফেলা হলে আলোর রশ্মিগুলো প্রতিফলনের পর এক বিন্দুতে মিলিত হবে। ৰুঝতেই পারছ এই কিছুটি অবতল আয়নার ফোকাস বিন্দু এবং মেরু বিন্দু থেকে এই বিন্দু পর্যন্ত দূরত্বটা হচ্ছে ফোকাস দূরত্ব। আলোর রশ্মির তো আর থেমে থাকার উপায় নেই কাজেই এক বিন্দুতে মিলিত হবার পরও সেটা সোজা সামনের দিকে এগোতে থাকবে এবং দেখা যাবে সেই বিন্দু থেকে আলোগুলো ছড়িয়ে পড়ছে। অর্থাৎ ফোকাস বিন্দুতে পৌঁছানোর আগে আলো একত্র হতে থাকে (অভিসারী) ফোকাস বিন্দুতে পৌঁছানোর পর আলো ছড়িয়ে যেতে থাকে (অপসারী)।
উত্তল আয়নার বেলাতেও আমরা একই উত্তর পেয়েছিলাম ,যার মানে ফোকাস দূরত্ব বাড়তে বাড়তে অসীম হয়ে গেলে উত্তল এবং অবতল আয়না দুটিই সমতল আয়না হয়ে যায়। উত্তল আয়নার মতো অবতল আয়নাতেও ফোকাস দূরত্ব হচ্ছে ব্যাসার্ধের অর্ধেক। এটি হুভু প্রমান করা যায় না ,কাছাকাছি প্রমানটি এবার আমরা তোমাদের হাতে ছেড়ে দিলাম।
এবারে এসেছি আমরা সবচেয়ে মজার অংশটুকুতে। সমতল আয়না এবং উত্তল আয়নায় শুধু একধরনের প্রতিবিম্ব তৈরি হতো। অবতল আয়নায় দুই ধরনের প্রতিবিম্ব হতে পারে। একটা বস্তু ফোকাস দূরত্ব থেকে কম দূরত্বে রাখলে একধরনের প্রতিবিম্ব তৈরি হয়, ফোকাস দূরত্ব থেকে বেশি দূরত্বে রাখলে অন্য রকম প্রতিবিম্ব তৈরি হয়।
সেটি শুরু করার আগে আমরা আলোক রশ্মি গোলীয় অবতল আয়নায় কীভাবে প্রতিফলিত হয় সেটি জেনে নেই। গোলীয় অবতল আয়নায় তিনটি বিশেষ আলোক রশ্মির প্রতিফলনের নিয়ম জানলেই কীভাবে প্রতিবিম্ব তৈরি হয় সেটি ব্যাখ্যা করতে পারব:
(i) আলোক রশ্মি ব্যাসার্ধ বরাবর বা কেন্দ্র থেকে শুরু হলে সেটি লম্বভাবে প্রতিফলিত হয়ে যেদিক থেকে এসেছে ঠিক সেদিকেই ফিরে যায়।
(ii) প্রধান অক্ষের সমান্তরাল রশ্মিটি প্রতিফলনের পর ফোকাস বিন্দু দিয়ে যাবে।
(iii) আলোক রশ্মির দিক পরিবর্তন করা হলে এটি যেদিক থেকে এসেছে ঠিক সেদিক দিয়ে ফিরে যায়। কাজেই কোনো আলোক রশ্মি ফোকাস দিয়ে গেলে সেটি প্রধান অক্ষের সাথে সমান্তরাল হয়ে প্রতিফলিত হবে।
এবারে আমরা অবতল আয়নার জন্য প্রতিবিম্ব তৈরি করতে পারব।
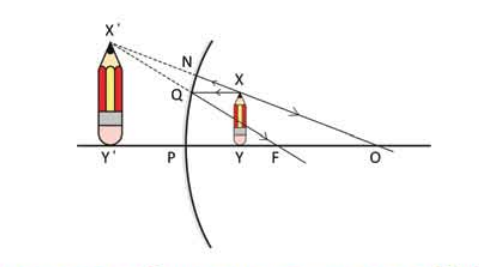
চিত্র 8. 22:অবতল আয়নায় একটি বস্তু ফোকাস দূরত্বের ভেতরে রাখা হলে প্রতিবিম্ব বড় দেখায়
8.07 চিত্রে একটি অবতল আয়না দেখানো হয়েছে। অবতল আয়নাটি যে গোলকের অংশ সেই গোলকের কেন্দ্র হচ্ছে O, অবতল আয়নার ফোকাস বিন্দু F এবং ধরা যাক XY বস্তুটির প্রতিবিম্বটি আমরা বের করতে চাই। Y বিন্দুটি থেকে আলো অবতল আয়নার P বিন্দুতে প্রতিফলিত হয়ে আবার Y হয়ে O বিন্দুর দিকে ফিরে যাবে। কাজেই বোঝা যাচ্ছে এটি OP রেখায় কিংবা তার বর্ধিত অংশের কোনো একটা বিন্দুতে থাকবে, ঠিক কোথায় সেই বিন্দুটি হবে সেটি বের করতে হলে Y বিন্দু থেকে অন্যদিকে আরো একটি রশ্মিকে অবতল আয়নার দিকে আঁকতে হবে, আমরা আর সেটি করছি না, আগের মতো X বিন্দুটির প্রতিবিম্ব বের করতে পারলেই সেখান থেকে Y বিন্দুটির প্রতিবিম্বের সঠিক জায়গাটি বের করা যাবে। X বিন্দুর প্রতিবিম্ব বের করতে হলে এই বিন্দু থেকে দুটি রেখা আঁকতে হবে, বোঝাই যাচ্ছে প্রথম রেখাটি হবে OX রেখার বর্ধিত অংশ, এটা অবতল আয়নাকে লম্বভাবে স্পর্শ করে ঠিক সেই পথেই প্রতিফলিত হয়ে ফিরে যাবে। চিত্রে যেভাবে দেখানো হয়েছে X বিন্দু থেকে আরেকটা রশ্মি হতে পারে অক্ষের সাথে সমান্তরাল একটা রশ্মি, কারণ আমরা এর মধ্যে জেনে গেছি সমান্তরাল রশ্মি প্রতিফলনের পর ফোকাস বিন্দু দিয়ে যায়। কাজেই এটা Q বিন্দুতে আপতিত হয়ে প্রতিফলিত হয়ে F বিন্দু দিয়ে চলে যাবে।
X বিন্দু থেকে বের হওয়া দুটি রশ্মি প্রতিফলনের পর NO এবং OF এর দিকে যাবে এবং দেখাই যাচ্ছে এই রশ্মি দুটো মিলিত হবার কোনো সুযোগ নেই। কাজেই ডান পাশে কোনো প্রতিবিম্ব তৈরি হতে পারবে না। কিন্তু যদি ডান পাশ থেকে বাম পাশে তাকানো যায় তাহলে মনে হবে ON রেখা এবং FQ রেখা দুটি বুঝি x' বিন্দুতে মিলিত হয়েছে— কাজেই x হবে X এর প্রতিবিম্ব। এই বিন্দু থেকে OP অক্ষের ওপর একটি লম্ব আঁকলেই আমরা XY এর পুরো প্রতিবিম্ব XY' পেয়ে যাব। x y থেকে সত্যিকারভাবে কোনো আলো যাচ্ছে না, শুধু আমাদের মনে হচ্ছে এখানে বুঝি প্রতিবিম্বটি তৈরি হয়েছে। কাজেই এই প্রতিবিম্বটি অবাস্তব প্রতিবিম্ব। চিত্র থেকে দেখা যাচ্ছে প্রতিবিম্বটি মূল বস্তু থেকে বড়। শুধু তা-ই নয় আমরা বস্তুটিকে যতই ফোকাস বিন্দুর কাছে আনব, প্রতিবিম্বটি ততই বড় হবে। (যদি এটাকে ঠিক ফোকাস বিন্দুতে বসানো হয় তাহলে প্রতিফলিত আলোক রশ্মি আসলে সমান্তরাল হয়ে যাবে অর্থাৎ প্রতিবিম্ব তৈরি করার জন্য আলোক রশ্মি আর মিলিত হতে পারবে না।
এবারে অবতল আয়নায় ফোকাস দূরত্বের ভেতরে কোনো কিছু রাখা হলে তার প্রতিবিম্বটি কেমন হবে সেটি দেখে নেওয়া যাক :
(a) প্রতিবিম্বটির অবস্থান কোথায় হবে সেটি নির্ভর করবে আসল বস্তুটির অবস্থানের ওপর। বস্তুটি যতই ফোকাসের কাছে রাখা হবে প্রতিবিম্বের অবস্থানটি হবে তত দূরে।
(b) এটি অবাস্তব
(c) সোজা
(d) প্রতিবিম্বটির দৈর্ঘ্যও নির্ভর করবে তার অবস্থানের ওপর, যত ফোকাস বিন্দুর কাছে যাবে তার দৈর্ঘ্যও তত বেড়ে যাবে।
আমরা এখন পর্যন্ত যত প্রতিবিম্ব দেখেছি তার মাঝে এই প্রতিবিম্বটি সবচেয়ে চমকপ্রদ, কারণ এই প্রথমবার আমরা একটি বাস্তব প্রতিবিম্ব দেখব, অর্থাৎ যেখানে প্রতিবিম্বটি তৈরি হবে, সেখানে সত্যি সত্যি আলো কেন্দ্ৰীভূত হবে(চিত্র 8.08)।
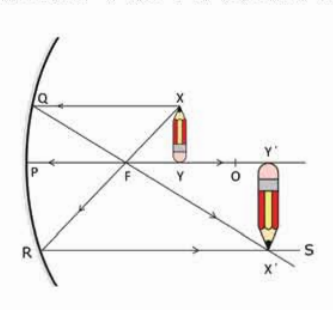
চিত্র 8.23: অবতল আয়নায় একটি বস্তু ফোকাস দূরত্বের বাইরে রাখলে প্রতিবিম্বটি হয় উল্টো।
সত্যিকারের বস্তুটি হচ্ছে XY এবং Y বিন্দুর প্রতিবিম্বটি অন্যবারের মতো নিশ্চয়ই YP রেখার উপরে থাকবে। x বিন্দুটির প্রতিবিম্ব বের করার জন্য আমাদের দুটি রশ্মি আঁকতে হবে। একটি হবে অক্ষের সাথে সমান্তরাল XQ এবং প্রতিফলিত হয়ে এটি নিশ্চয়ই ফোকাস বিন্দু F এর ভেতর দিয়ে QF হিসেবে যাবে। দ্বিতীয় রশ্মিটি আমরা F বিন্দুর ভেতর দিয়ে আঁকতে পারি। এটি অবতল আয়নার প্রতিফলিত হয়ে RS হিসেবে সমান্তরাল হয়ে যাবে, কারণ সমান্তরাল রেখার আলো অবতল আয়নাতে প্রতিফলিত হয়ে যে রকম ফোকাস বিন্দুর ভেতর দিয়ে যার ঠিক সে রকম তার উল্টোটাও সত্যি, আলো সব সময়ই তার গতিপথ উল্টো পথে পুরোপুরি অনুসরণ করে। QF এবং RS রেখা দুটি X' বিন্দুতে ছেদ করেছে এবং X' বিন্দুটি হচ্ছে X বিন্দুর প্রতিবিম্ব। কাজেই X' বিন্দু থেকে PO রেখার ওপর লম্বটি Y' বিন্দুতে ছেদ করেছে এবং X'Y' হচ্ছে XY এর প্রতিবিম্ব। দেখতেই পাচ্ছ এই প্রতিবিম্বটি এখন পর্যন্ত দেখা অন্যান্য প্রতিবিম্ব থেকে ভিন্ন।
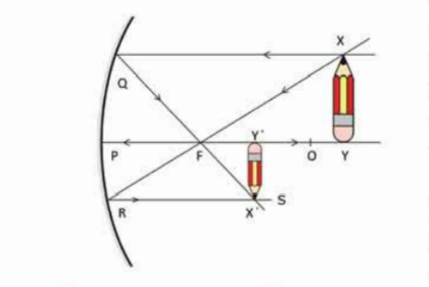
চিত্র 8.24:অবতল আয়নায় একটি বস্তু ফোকাস দূরত্বের বাইরে রাখলে প্রতিবিম্বটি
উল্টো এবং ছোট হয়।
8.24 চিত্রে হুবহু একই বিষয় দেখানো হয়েছে।শুধু XY বস্তুটি ফোকাস দূরত্বের দ্বিগুণ থেকে বেশি দুরত্বে রাখা হলে এবারে বস্তুটির প্রতিবিম্বটি হবে ছোট।বস্তুটি যদি ঠিক ফোকাস দূরত্বের দ্বিগুণ দূরত্বে রাখা হতো তাহলে তার প্রতিবিম্বটিও হতো এই একই বিন্দুতেে। শুধু তা-ই নয়, প্রতিবিম্বটির আকার হতো ঠিক বস্তুটির সমান। ফোকাস দূরত্বের বাইরে রাখা এই তিনটি ভিন্ন ভিন্ন ব্যাপার এবারে গুছিয়ে লেখা যেতে পারে। ফোকাস দূরত্বের বাইরে কোনো বস্তুকে রাখা হলে তার প্রতিবিম্ব হবে এ রকম:
(a) প্রতিবিম্বের অবস্থানটা নির্ভর করবে বস্তুটি কোথায় আছে তার ওপর। যতক্ষণ পর্যন্ত বস্তুটি ফোকাস বিন্দু এবং অবতল আয়নার কেন্দ্রের মাঝখানে আছে প্রতিবিম্বের অবস্থানটা হবে কেন্দ্রের বাইরে। বস্তুটি যদি অবতল আয়নার বক্রতার কেন্দ্র থেকে বাইরে থাকে তাহলে তার প্রতিবিম্ব হবে কেন্দ্রের ভেতরে। যদি বস্তুটি ঠিক কেন্দ্রের ওপর থাকে তাহলে প্রতিবিম্বের অবস্থানটাও হবে কেন্দ্রে।
(b) প্রতিবিম্বটি বাস্তব। তাই বস্তুটাকে দিয়ে তার প্রতিবিম্ব যে রকম বের করতে পারি ঠিক সেরকম প্রতিবিম্বটাকে বস্তু ধরা হলে বস্তুটাই হবে তার প্রতিবিম্ব।
(c) প্রতিবিম্বটি উল্টো।
(d) প্রতিবিম্বটির দৈর্ঘ্য নির্ভর করবে এটি কোথায় আছে তার ওপর। যদি এটা ফোকাস বিন্দু এবং বক্রতার কেন্দ্রের মাঝখানে থাকে তাহলে প্রতিবিম্বটির প্রতিবিম্ব হবে বস্তুটি থেকে বড়। যত ফোকাস বিন্দুর কাছাকাছি তত বড়। যদি বস্তুটি বক্রতার কেন্দ্র থেকে বাইরে হয় তাহলে এর আকার হবে আসল বস্তুটি থেকে ছোট। যদি এটা ঠিক বক্রতার কেন্দ্রে থাকে তাহলে প্রতিবিম্বের আকার হবে ঠিক বস্তুটির আকারের সমান।
আমরা জ্যামিতি ব্যবহার করে উত্তল এবং অবতল আয়নার জন্য প্রতিবিম্বের অবস্থান আকার ইত্যাদি বের করেছি। আমরা চাইলে একটিমাত্র সূত্র ব্যবহার করে এই কাজগুলো করতে পারতাম, সূত্রটি হচ্ছে:
1u+1v=1f
এখানে u হচ্ছে আয়নার পৃষ্ঠ থেকে বস্তুর দূরত্ব, v হচ্ছে প্রতিবিম্বের দূরত্ব এবং f হচ্ছে ফোকাস দূরত্ব।
বাস্তব প্রতিবিম্ব খুবই গুরুত্বপূর্ণ একটি ধারণা। আমরা পরের অধ্যায়ে দেখব কেমন করে লেন্স দিয়েও এ রকম বাস্তব প্রতিবিম্ব তৈরি করা যায়। তোমরা দেখতেই পেয়েছ বাস্তব প্রতিবিম্বে সত্যিকারের আলোক রশ্মি থাকে, তাই এটাকে যদি কোনো পর্দায় ফেলা যায়, সেখানে প্রতিবিম্বটি দেখাও সম্ভব হয়। সাধারণ আয়নায় তুমি তোমার চেহারা দেখতে পারবে কিন্তু শুধু সাধারণ আয়না দিয়ে কখনো তোমার চেহারা কোনো পর্দায় ফেলতে পারবে না।
আমরা যেহেতু দেখতে পেরেছি যে একটা প্রতিবিম্ব কখনো প্রকৃত বস্তু থেকে ছোট হয় কখনো বড় হয় তাই বিষয়টিকে ব্যাখ্যা করার জন্য বিবর্ধন বলে একটা শব্দ ব্যবহার করা যেতে পারে। প্রতিবিম্বটি মূল বস্তু থেকে কত বড় সেটাকে বিবর্ধন m বলা হয়। যদি একটা বস্তুর আকার হয় l এবং তার প্রতিবিম্বের আকার হয়।' তাহলে বিবর্ধন হচ্ছে
m=l'l
আমরা যখন টেলিস্কোপে কোনো বস্তুকে দেখি, খালি চোখে দেখলে সেটাকে যত বড় দেখানোর কথা টেলিস্কোপে দেখলে সেটাকে সে তুলনায় যত বড় দেখাবে, সেটাই হচ্ছে টেলিস্কোপের বিবর্ধন।
দৈনন্দিন জীবনে সাধারণ আয়নার ব্যবহার সবচেয়ে বেশি। যখনই একদিকে পাঠানো আলোকে অন্যদিকে নিতে হয় তখন আমরা সাধারণ আয়না ব্যবহার করি। তোমরা নিশ্চয়ই লক্ষ করেছ সাধারণ আয়নায় ডান এবং বাম দিক বদলে যায়। তাই যদি আমাদের ডান-বাম অবিকৃত রাখতে হয় তাহলে একটি আয়নার প্রতিবিম্ব অন্য একটি আয়নার দ্বিতীয়বার প্রতিফলিত করে আবার ঠিক করে নিতে হয়।
সাধারণ আয়নার প্রতিবিম্ব ডান এবং বামের পরিবর্তন হয়। দুটি আয়নাকে পরস্পরের সাথে 90° তে রেখে সেটাকেই একটা আয়না হিসেবে ব্যবহার করলে ডান-বামের পরিবর্তন হয় না। দুটি আয়না দিয়ে বিষয়টা পরীক্ষা করে দেখো(8.26) ।
এখানে একটা খুব গুরুত্বপূর্ণ বিষয় জেনে রাখা ভালো, যখন খুব ভালো প্রতিফলনের প্রয়োজন হয় তখন কিন্তু সাধারণ আয়না ব্যবহার না করে সম্পূর্ণ ভিন্ন এক ধরনের প্রতিফলন করা হয়। আমরা পরের অধ্যায়ে দেখব পুরোপুরি স্বচ্ছ মাধ্যম দিয়ে কীভাবে আলোকে প্রতিফলিত করা যায়। আমরা পরের অধ্যায়ে দেখব পুরোপুরি স্বচ্ছ মাধ্যম দিয়ে কিভাবে আলোক প্রতিফলিত করা যায় ।
উত্তল আয়নায় যেহেতু সোজা এবং ছোট প্রতিবিম্ব তৈরি করা যায় ভাই বড় কোনো দৃশ্যকে ছোট জায়গায় দেখতে হলে উত্তল আরনা ব্যবহার করা হয়। গাড়ির দক্ষ ড্রাইভাররা গাড়ি চালানোর সময় সব সময় পেছনে কী হচ্ছে দেখার চেষ্টা করেন, সে জন্য গাড়ির ড্রাইভারের সামনে রিয়ার ভিউ মিরর থাকে। এই মিররগুলোতে উত্তল আয়না ব্যবহার করা হয় যেন ছোট একটা আয়না দিয়েই গাড়ির ড্রাইভাররা পেছনের বড় একটা জায়গা দেখতে পারেন।
অবতল আয়নার সবচেয়ে বড় ব্যবহার হচ্ছে টেলিস্কোপে। পৃথিবীর সবচেয়ে বড় এবং সবচেয়ে সুক্ষ্ম টেলিস্কোপে অবতল আয়না ব্যবহার করা হয় । অনেকে সাধারণভাবে মনে করে দুরের কোনো ছোট জিনিসকে অনেক বড় করে দেখানোই বুঝি ভালো টেলিস্কোপের দায়িত্ব। আসলে সেটি সত্যি নয়, ভালো টেলিস্কোপের দায়িত্ব অনেক কম আলোতেও স্পষ্ট প্রতিবিম্ব তৈরি করা। সেজন্য অবতল আয়নার আকার যত বড় হবে, সেটি তত বেশি আলো সংগ্রহ করে তত স্পষ্ট প্রতিবিম্ব তৈরি করতে পারবে। পৃথিবীর সব বড় বড় টেলিস্কোপে অবতল আরনা ব্যবহার করা হয়।
অবতল আয়নার আরেকটি ব্যবহার হচ্ছে আলোকের সমান্তরাল বিম তৈরি করা। জাহাজ বা লঞ্চের সার্চলাইটে অবতল আয়না ব্যবহার করা হয়। আলোর উৎসটুকু থাকে ফোকাস বিন্দুতে তাই সেটি অবতল আয়নায় প্রতিফলিত হয়ে সমান্তরাল বিষ হিসেবে বের হয়ে যায়। তোমরা দৈনন্দিন জীবনে যে টর্চলাইট ব্যবহার করো সেখানেও বাহুটি রাখা হয় একটি অবতল আয়নার ফোকাস বিন্দুতে।
অবতল আয়নায় ফোকাস দূরত্বের ভেতরে কিছু থাকলে যেহেতু সোজা এবং বড় প্রতিবিম্ব তৈরি হয় ভাই কোনো কিছু বড় করে দেখতে হলেও অবতল আয়না ব্যবহার করা হয়। ডাক্তার কিংবা ডেন্টিস্টরা তাই অনেক সময়ই কিছু দেখার জন্য অবতল আয়না ব্যবহার করেন।
একটি দেশ যখন উন্নত হতে শুরু করে তখন প্রথমেই তার যোগাযোগ ব্যবস্থাকে উন্নত করতে হয়। রাস্তাঘাট তৈরি করতে হয় এবং সেই রাস্তাঘাট দিয়ে নানা ধরনের যানবাহন চলতে শুরু করে। তোমরা নিশ্চয়ই দেখেছ আমাদের দেশের রাস্তাঘাট দিয়ে কত ধরনের যানবাহন যায় এবং প্রতিদিনই তার সংখ্যা কীভাবে বেড়ে যাচ্ছে। রাস্তাঘাট যথেষ্ট না হওয়ায় ট্রাফিক জ্যামে আমাদের প্রচুর সময় নষ্ট হয় এবং দূরপাল্লার যানবাহনে গাড়ি দুর্ঘটনায় অনেক মানুষের মৃত্যু হয়। এই মৃত্যুর একটি বড় কারণ আমাদের ড্রাইভাররা অনেক সময়ই নিরাপদ ড্রাইভিং না করে দ্রুত এক জায়গা থেকে অন্য জায়গায় যেতে চায়। নিরাপদ ড্রাইভিংয়ের জন্য অনেক ধরনের সচেতনতা দরকার, তার মাঝে আলোর সঠিক ব্যাপার একটি।
গাড়ি চালানোর সময় ব্রেক লাইট একটা গুরুত্বপূর্ণ ভূমিকা রাখে, এই লাইট দেখে পেছনের গাড়ির ড্রাইভার বুঝতে পারে সামনের ড্রাইভার তার গতি কমাতে যাচ্ছে, গাড়ি কোনদিকে যাবে কিংবা লেন পরিবর্তন করবে কি না। সেটা অন্যদের জানানোর জন্য টার্ন লাইট ব্যবহার করা হয়। গাড়ির সামনের হেড লাইট অন্ধকার রাস্তা আলোকিত করে, কিন্তু সেটি ব্যবহারের একটা সুনির্দিষ্ট নিয়ম আছে, বিপরীত থেকে একটা গাড়ি আসতে থাকলে তীব্র আলোতে যেন তার চোখ ধাঁধিয়ে না যায় সেজন্য কখনোই হাই বিম অন করতে হয় না। একজন ড্রাইভার যখন গাড়ি চালায় তখন শুধু সামনে নয়, পেছনে এবং পাশে কোন যানবাহন আছে সেটি জানতে হয়। সেজন্য ড্রাইভারের সামনে রিয়ার ভিউ মিরর এবং দুই পাশে সাইডভিউ মিরর থাকে। ছোট আয়নাতে যেন অনেকটুকু জায়গা দেখা যায় সেজন্য এই আয়নাগুলো হয় অবতল। একজন ভালো ড্রাইভার যখন গাড়ি চালায় সে শুধু সামনের যানবাহন নয় পাশে এবং পেছনের যানবাহন নিয়েও সব সময় সজাগ থাকে।
পাহাড়ি রাস্তা সাধারণত আঁকাবাঁকা হয় আবার একই সাথে উঁচু-নিচু হয়। শুধু তাই নয়, অনেক সময়ই রাস্তার এক পাশে উঁচু পাহাড় অন্য পাশে গভীর খাদ থাকে। কাজেই পাহাড়ি রাস্তায় গাড়ি চালানোর সময় অনেক সতর্ক থাকতে হয়। তারপরও স্থানে স্থানে গাড়ি চালানো ঝুঁকিপূর্ণ হতে পারে। বিশেষ করে যখন প্রায় সমকোণে বাঁক নিতে হয় তখন রাস্তার অন্য পাশ দিয়ে কী আসছে সেটা জানার কোনো উপায় থাকে না। এরকম অবস্থায় বাঁকগুলোতে 45° কোণে বড় আকারের সমতল আয়না বসানো হয়। তখন রাস্তার দুই পাশের সব যানবাহনই রাস্তার অন্য পাশে কী আছে সেটি দেখতে পায় এবং রাস্তায় গাড়ি চালানো তুলনামূলকভাবে নিরাপদ হয়ে যায়।
Read more