নানা ধরনের কাজের জন্য আমরা নানা ধরনের শক্তি ব্যবহার করি। যেমন পানি গরম করার জন্য তাপ শক্তির প্রয়োজন হয়, দেখার জন্য আমাদের আলো শক্তি লাগে, আমরা শুনি শব্দ শক্তি দিয়ে। বৈদ্যুতিক শক্তি দিয়ে আমরা যন্ত্রপাতি চালাই আবার রাসায়নিক শক্তি ব্যবহার করে তড়িৎ কোষ বিদ্যুৎ তৈরি করি। ভারী নিউক্লিয়াস ভেঙে বা হালকা নিউক্লিয়াস জোড়া দিয়ে আমরা যে নিউক্লিয়ার শক্তি পাই সেটা দিয়েও বিদ্যুৎ শক্তি তৈরি করি। খাবার থেকে পুষ্টি নিয়ে আমাদের শরীরে শক্তি তৈরি হয়, আমরা কাজকর্ম করি।
আমাদের সভ্যতার ইতিহাসটিই হচ্ছে শক্তি তৈরি করে সেই শক্তি ব্যবহারের ইতিহাস। আমরা আমাদের চারপাশে সেই শক্তির নানা রূপকে দেখতে পাই, যেমন— যান্ত্রিক শক্তি, তাপ শক্তি, শব্দ শক্তি, আলোক শক্তি, চৌম্বক শক্তি, বিদ্যুৎ শক্তি, রাসায়নিক শক্তি, নিউক্লিয় শক্তি এবং সৌর শক্তি।
শক্তির সবচেয়ে সাধারণ রূপ হচ্ছে যাত্মিক শক্তি, বস্তুর অবস্থান, আকার এবং গতির কারণে যে শক্তি পাওয়া যায় তাকেই যান্ত্রিক শক্তি বলে। যান্ত্রিক শন্তির দুটি রূপ হতে পারে গতিশক্তি এবং স্থিতিশক্তি।
আমরা আগে বলেছি কাজ করার সামর্থ্য হচ্ছে শক্তি। আমরা সবাই জানি কোনো বস্তু গতিশীল হলে সেটা অন্য বস্তুকে ধাক্কা দিয়ে সেটাকেও গতিশীল করে খানিকটা দূরত্ব ঠেলে নিয়ে যেতে পারে। অন্য বস্তুকে গতিশীল করে ফেলার অর্থ নিশ্চরই সেখানে বল প্ররোগ হয়েছে এবং সেই বলের জন্য খানিকটা দূরত্ব যাওয়ার অর্থ নিশ্চয়ই সেখানে কাজ হয়েছে। কাজেই আমরা নিশ্চিতভাবে বলতে পারি
গতির জন্য বস্তুর যে শক্তি হয় সেটা নিশ্চয়ই এক ধরনের শক্তি বা গতিশক্তি। আগের অধ্যায়ে আমরা বলেছি যে আমরা রাস্তাঘাটে যে ভয়ংকর দুর্ঘটনা ঘটতে দেখি সেখানে যে ক্ষয়ক্ষতি হয় তার প্রধান কারণ এই গতিশক্তি। একটা বাস-ট্রাক বা গাড়ি যখন প্রচণ্ড বেগে ছুটতে থাকে তখন তার অনেক বড় গতিশক্তি থাকে। দুঘর্টনার সময় এই পুরো শক্তিটার কারণে গাড়ি ভেঙেচুরে যায়, প্রচণ্ড ধাক্কায় মানুষ মারা যায়।
একটা বস্তুর উপর বল প্রয়োগ করে কাজ করা হলে সেখানে কতটুকু গতিশক্তি হবে সেটা আমরা খুব সহজে বের করতে পারি।
ধরা যাক F বল প্রয়োগ করে m ভরের একটা বস্তুকে s দূরত্ব সরানো হলো। তাহলে এই F বলের সম্পাদিত কাজ W হচ্ছে
নিউটনের দ্বিতীয় সূত্র থেকে আমরা জানি F = ma গতির সমীকরণ থেকে আমরা জানি স্থির অবস্থা থেকে শুরু করা হলে
এবং
কাজ
কাজেই আমরা বলতে পারি F বল কোনো বস্তুকে s দূরত্বে নিয়ে গেলে তার ভেতরে যে শক্তির সঞ্চার হয় সেটি
হচ্ছে
গতিশক্তিতে v টি বর্গ হিসেবে আছে, কাজেই কোনো বস্তুর গতিশক্তিকে দ্বিগুণ বাড়াতে আমাদের চার গুণ বেশি শক্তি দিতে হয়।
গতির সমীকরণ শেখার সময় আমরা দেখেছিলাম
দুইপাশে ½m দিয়ে গুণ করলে সূত্রটি দাঁড়ায়:
ma এর পরিবর্তে যদি আমরা F লিখি এবং Fs এর পরিবর্তে W লিখি তাহলে সূত্রটি দাঁড়ায়:
অর্থাৎ কোনো বস্তু যদি u বেগে থাকে তাহলে তার গতি এবং তার উপর W কাজ করা হলে গতিশক্তি বেড়ে হয় গতির এই সমীকরণটি উল্লেখ করার সময় আমরা বলেছিলাম যে পরে আমরা এর একটি চমকপ্রদ রূপ দেখব। এটি হচ্ছে সেই রূপ অর্থাৎ গতির সমীকরণটি আসলে গতিশক্তির একটি সমীকরণ ছাড়া কিছু নয়।
কাজ সম্পর্কে বলতে গিয়ে আমরা বলেছিলাম যখন কোনো বল কোনো কিছুর ওপর পজিটিভ কাজ করে তখন সেখানে শক্তির সৃষ্টি হয়। গতিশক্তি সম্পর্কে বলার সময় আমরা তার একটা উদাহরণও দিয়েছিলাম, দেখিয়েছিলাম একটা বস্তুর ওপর বল প্রয়োগ করে সেটাকে খানিকটা দূরত্বে নিয়ে গেলে গতিশক্তি বেড়ে যায়।
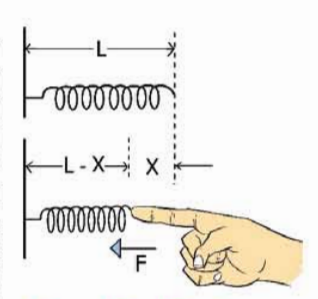
চিত্র 4.01: স্প্রিংয়ের স্থিরাবস্থা এবং বল প্রয়োগ করে সংকুচিত করা
এবারে এমন একটা উদাহরণ দেওয়া হবে, যেখানে বল প্রয়োগ করে খানিকটা দূরত্ব অতিক্রম করার পরও কোনো গতিশক্তি তৈরি হবে না। মনে করো টেবিলে একটা স্প্রিং 4.01 চিত্রে দেখানো উপায়ে রাখা আছে, তুমি স্প্রিংরের খোলা মাথার আঙুল দিয়ে F বল প্রয়োগ করে স্প্রিংটাকে x দূরত্বে সংকুচিত করে দিয়েছ। এ রকম অবস্থায় তোমার হাত বা স্প্রিং কোনোটাই গতিশীল না, তাই কোথাও কোনো গতিশক্তি নেই! যেহেতু যেদিকে F বল প্রয়োগ করা হয়েছে অতিক্রান্ত দূরত্বও সেই দিকে, তাই কাজটি পজিটিভ, আমাদের কাজের সংজ্ঞা অনুযায়ী এখানে শক্তি সৃষ্টি হওয়ার কথা। কিন্তু সেই শক্তিটি কোথায়? কোনো কিছু গতিশীল নয়, তাই এখানে নিশ্চিতভাবে কোনো গতিশক্তি।
আমরা যারা স্প্রিং ব্যবহার করেছি তারা অনুমান করতে পারছি যে সংকুচিত স্প্রিংয়ের ভেতর নিশ্চয়ই শক্তিটুকু লুকিয়ে রয়েছে। কারণ আমরা জানি সংকুচিত স্প্রিংটার সামনে একটা m ভরের বস্তু রেখে স্প্রিংটা ছেড়ে দিলে স্প্রিংটা ভরটার ওপর বল প্রয়োগ করে একটা দূরত্ব অতিক্রম করাতে পারত, যার অর্থ কাজ করাতে পারত। অর্থাৎ এটি একটি শক্তি, গতিশক্তি না হলেও এটি অন্য এক ধরনের শক্তি। এই ধরনের সঞ্চিত শক্তিকে বলে বিভব শক্তি (Potential Energy)। এই শক্তিটি কোনো বস্তুর অবস্থা বা অবস্থানের জন্য তৈরি হয়।
একটি স্প্রিংয়ের ধ্রুবক যদি হয় এবং স্প্রিংটিকে যদি তার স্থির অবস্থার সাপেক্ষে x দূরত্ব সংকুচিত করা হয় তাহলে তার ভেতরে শক্তি সঞ্চিত হয়
আমরা যখন কোনো কিছুকে উপরে তুলি তখনো সেটা বিভব শক্তি অর্জন করে। এক টুকরো পাথর ওপর থেকে ছেড়ে দিলে সেটা নিচে নামার সময় তার গতি বাড়তে থাকে তাই সেটার মাঝে গতিশক্তির জন্ম হয়। এটি সম্ভব হয় কারণ পাথরটা যখন উপরে ছিল তখন এই “উপরে অবস্থানের জন্য তার মাঝে এক ধরনের বিভব শক্তি জমা হয়েছিল। একটা পাথরকে উপরে তোলা হলে তার ভেতরে কী পরিমাণ বিভব শক্তি জমা হয়, এখন সেটাও আমরা বের করতে পারি। বুঝতেই পারছ একটা বস্তুকে উপরে তুলতে হলে যে পরিমাণ কাজ করতে হয় সেটাই বিভব শক্তি হিসেবে পাথরের মাঝে জমা হয়ে যাবে। কাজের পরিমাণ W হলে
এখানে F হচ্ছে প্রযুক্ত বল এবং h হচ্ছে উচ্চতা। F বলটি আমাদের প্রয়োগ করতে হয় উপরের দিকে এবং অতিক্রান্ত দূরত্বও উপরের দিকে, কাজেই পজিটিভ। উপরে তোলার জন্য যে বল প্রয়োগ করতে হয় তার মান স্প্রিংয়ের বলের মতো পরিবর্তন হয় না এবং এই বলটি পাথরটির ওজনের সমান। পাথরটির ওজন mg হলে
এবং
মনে রাখতে হবে, পাথরটির ওজন একটি বল এবং সেটি নিচের দিকে কাজ করে। পাথরটাকে উপরে তুলতে হলে এই ওজনের সমান একটা বল আমাদের উপরের দিকে প্রয়োগ করতে হয়।
m ভরের একটা পাথরকে h উচ্চতার তুলে তার ভেতরে বিভব শক্তি সৃষ্টি করে যদি পাথরটাকে ছেড়ে দিই তাহলে সেটা যখন নিচের দিকে / দূরত্ব নেমে আসবে, তখন তার ভেতরে কী পরিমাণ গতিশক্তি জন্ম নেবে?
শক্তির নিত্যতার কারণে তার বিভব শক্তির পুরোটুকুই গতিশক্তিতে পরিণত হবে। আমরা জানি গতিশক্তি হচ্ছে ½ mv2 তাই আমরা লিখতে পারি:
সত্যি কথা বলতে কি আমরা পড়ন্ত বস্তুর সমীকরণ বের করার সময় হুবহু এই সূত্রটি ইতিমধ্যে একবার বের করেছিলাম। শক্তির ধারণা দিয়ে সম্পূর্ণ অন্যভাবে আমরা আবার একই সূত্র বের করেছি |