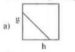
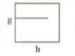
অভিকর্ষীয় ত্বরণে g বনাম পৃথিবী পৃষ্ঠ হতে গভীরতা h এর লেখচিত্র কোনটি?


মহাকর্ষীয় ধ্রুবকের মান নির্ণয়ের জন্য অনেকগুলো পদ্ধতি আছে। তবে এখানে আমরা ক্যাভেন্ডিসের পদ্ধতি আলোচনা করব ।
1798 খ্রিস্টাব্দে বিজ্ঞানী ক্যাভেন্ডিস মহাকর্ষীয় ধ্রুবকের মান নির্ণয়ের জন্য একটি ব্যবর্ত তুলা পদ্ধতি উদ্ভাবন করেন। তাঁর নাম অনুসারে এই পদ্ধতিকে ক্যাভেন্ডিসের পদ্ধতি বলা হয়।
এই যন্ত্রে সীসার তৈরি চারটি গোলক (A, B, C ও D) আছে। এদের মধ্যে A ও B ছোট এবং C ও D দুটি বড় গোলক[চিত্র ৭.২] । C এবং D একটি অনুভূমিক দণ্ড PQ-এর দু'প্রান্ত হতে ঝুলান হয়েছে। দণ্ডটি একটি উল্লম্ব অক্ষ XX'-এর সাথে যুক্ত থাকে। এই অক্ষ একটি চাকা W-এর সঙ্গে যুক্ত থাকে। চাকাটি বাহির হতে ঘুরানোর ব্যবস্থা থাকে। এর কিছুটা নিচে একই অক্ষে একটি ব্যবর্তন শীর্ষ ( torsion head) H হতে ব্যবর্তন তারের (T) সাহায্যে একটি হাল্কা দণ্ড RS ঝুলান আছে। RS-এর দু'প্রান্ত হতে দুটি ছোট সমান ভরের গোলক A ও B ঝুলান আছে। A, B এবং C, D একই অনুভূমিক তলে থাকে। T ব্যবর্তন তারের সাথে একটি দর্পণ (E) লাগানো থাকে। একটি আলোক উৎস (L) হতে দর্পণের উপর আলোক রশ্মি আপতিত করানো হয় এবং প্রতিফলিত রশ্মি একটি স্কেলের (S) উপর নিক্ষেপ করানো হয়। স্কেলের উপর প্রতিফলিত আলোক রশ্মির সরণ পরিমাপ করে ব্যবর্তন তারের মোচড় কোণ পরিমাপ করা হয়।
প্রথমে চাকা W-এর সাহায্যে PQ দণ্ডকে ঘুরিয়ে বড় গোলক দুটিকে দূরে সরিয়ে নেয়া হয় যাতে ছোট গোলকের উপরে প্রভাব না পড়ে। এই অবস্থায় স্কেলে দর্পণ E হতে প্রতিফলিত রশ্মির অবস্থানের পাঠ নেয়া হয়। এরপর বড় গোলক দুটিকে ছোট গোলক দুটির কাছাকাছি অবস্থানে আনা হয়। প্রত্যেক বড় গোলক (C বা D) তার নিকটে অবস্থিত ছোট গোলকের (A বা B) উপর একটি আকর্ষণ বল প্রয়োগ করে। সমান ও বিপরীতমুখী এই দুটি বল একটি বিক্ষেপী দ্বন্দ্বের (deflecting couple) সৃষ্টি করে যার ফলে RS দন্ডটি একটি ক্ষুদ্র কোণে ঘুরতে বাধ্য হয়। সুতরাং ব্যবর্তন তারে পাক পড়ে। তারটি এর স্থিতিস্থাপকতা ধর্মের জন্য বিপরীতমুখী প্রত্যায়নী দ্বন্দ্বের (restoring couple) সৃষ্টি করে দণ্ডটিকে পূর্বের অবস্থানে ফিরিয়ে নিতে সচেষ্ট হয়। দুটি পরস্পর বিপরীতমুখী দ্বন্দ্বের ক্রিয়ায় দণ্ডটি একটি সাম্য অবস্থানে আসে। এই অবস্থায় স্কেলে দর্পণ হতে প্রতিফলিত রশ্মির নতুন অবস্থানের পাঠ নেয়া হয়। প্রথম পাঠ ও দ্বিতীয় পাঠের পার্থক্য হতে দণ্ডের কৌণিক বিক্ষেপ নির্ণয় করা হয়। এরপর বড় গোলক দুটির অবস্থান [চিত্র ৭.৩] পূর্ব অবস্থান (K, m)-এর বিপরীত পার্শ্বে করা হয়।[চিত্রে K', m´ অবস্থান]। এভাবে ঘুরিয়ে দণ্ডের কৌণিক বিক্ষেপের মান বের করা হয়। পরিশেষে এই দুটি বিক্ষেপের গড় মান নির্ণয় করা যায় ।
মনে করি,
প্রত্যেকটি বড় গোলকের ভর =M
প্রত্যেকটি ছোট গোলকের ভর = m
RS দণ্ডের দৈর্ঘ্য = 2l
দণ্ডটির সাম্যাবস্থায় বড় ও ছোট্ গোলকের কেন্দ্রবিন্দুর মধ্যবর্তী দূরত্ব = d
A ও C গোলকের মধ্যকার আকর্ষণ বল,
B এবং D গোলক দুটির মধ্যে অনুরূপ আকর্ষণ বল বিদ্যমান আছে। এই দুটি সমান ও বিপরীতমুখী বল একটি দ্বন্দ্বের সৃষ্টি করে ।
অতএব, ব্যবর্তন শীর্ষ H সাপেক্ষে বিক্ষেপী দ্বন্দ্বের মোমেন্ট
দন্ডটি যদি '' কোণে বিচ্যুত হয় তাহলে মোচড়ের জন্য ব্যবর্তন তারে (T)
প্রত্যায়নী দ্বন্দ্বের মোমেন্ট =
এখানে = প্রতি ডিগ্রী বিক্ষেপের জন্য প্রত্যায়নী দ্বন্দ্বের মোমেন্ট।
সাম্যাবস্থায়, বিক্ষেপী দ্বন্দ্বের মোমেন্ট = প্রত্যায়নী দ্বন্দ্বের মোমেন্ট।
বা,
:-
এখন , d, 2l, M এবং m পরীক্ষা হতে জানা যায়। -এর মান জানা থাকলেই G-এর মান পাওয়া যাবে।
-এর মান নির্ণয় করার জন্য বড় দুটি গোলককে সরিয়ে ফেলি। তারপর ছোট দুটি গোলকসহ RS দণ্ডকে ব্যবর্তন তার T-এর সাপেক্ষে ব্যবর্তন দোলনে দোলাই এবং দোলনকাল নির্ণয় করি। যদি দোলনকাল T হয়, তবে,
বা,
সমীকরণ (6) হতে পাই,
সমীকরণ (7)-এর ডান পাশের সকল রাশির মান জানা থাকায় G-এর মান বের করা যায়। বিজ্ঞানী ক্যাভেন্ডিস এ পরীক্ষা বারবার পুনরাবৃত্তি করেন এবং G-এর গড় মান বের করেন। এর লব্ধ মান হল
G = (6.754 0.41) × 10-11 N-m² kg-2