Summary
প্রযুক্ত গণিতের বিভিন্ন উপপাদ্যের উপর আলোচ্য এই সামারি বিভিন্ন ত্রিভুজের সমতা প্রমাণ করে। এখানে মূল পয়েন্টগুলি তুলে ধরা হলো:
- প্রথম উপপাদ্য: CD, AB এর লম্ব সমদ্বিখণ্ডক। প্রমাণ: ∆ADC ≅ ∆BDC।
- দ্বিতীয় উপপাদ্য: CD = CB এবং ∠DCA = ∠BCA। প্রমাণ: AB = AD।
- তৃতীয় উপপাদ্য: ∠BAC = ∠ACD এবং AB = DC। প্রমাণ: AD = BC, ∠CAD = ∠ACB, ∠ADC = ∠ABC।
- চতুর্থ উপপাদ্য: সমদ্বিবাহু ত্রিভুজে অপর বাহু উভয় দিকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণগুলি সমান।
- পঞ্চম উপপাদ্য: AD = AE, BD = CE এবং ∠AEC = ∠ADB। প্রমাণ: AB = AC।
- ষষ্ট উপপাদ্য: ∆ABC এবং ∆DBC সমদ্বিবাহু। প্রমাণ: ∆ABD = ∆ACD।
- সপ্তম উপপাদ্য: সমদ্বিবাহু ত্রিভুজের ভূমির প্রান্তবিন্দু থেকে বিপরীত বাহুদের উপর অঙ্কিত মধ্যমাদ্বয় সমান।
- অষ্টম উপপাদ্য: সমবাহু ত্রিভুজের কোণগুলো সমান।
উপপাদ্য ৩: যদি একটি ত্রিভুজের তিন বাহু অপর একটি ত্রিভুজের তিন বাহুর সমান হয়, তবে ত্রিভুজ দুটি সর্বসম হবে।
উপপাদ্য ৪: দুটি কোণ ও সংলগ্ন বাহুর সমান হলে দুই ত্রিভুজ সম হবে।
উপপাদ্য ৫: একটি বাহু ও দুটি কোণ সমান হলে ত্রিভুজ দুটি সর্বসম হবে।
উদাহরণ ১: শিরঃকোণের সমদ্বিখণ্ডক যদি ভূমির উপর লম্ব হয়, তবে ত্রিভুজটি সমদ্বিবাহু।
উপপাদ্য ৫ (সমকোণী অতিভুজ-বাহু): দুটি সমকোণী ত্রিভুজের অতিভুজদ্বয় সমান হলে এবং একটির এক বাহু অপরটির এক বাহুর সমান হলে, ত্রিভুজদ্বয় সর্বসম হবে।
এগুলো বিভিন্ন ত্রিভুজের সমতার সম্বন্ধে মৌলিক তত্ত্ব উপস্থাপন করে এবং গণিতের জন্য গুরুত্বপূর্ণ উপপাদ্য।
১। চিত্রে, CD, AB এর লম্ব সমদ্বিখণ্ডক, প্রমাণ কর যে ADC ≅ ∠BDC

২। চিত্রে, CD = CB এবং ∠DCA = ∠BCA প্রমাণ কর যে, AB = AD

৩। চিত্রে, ∠BAC = ∠ACD এবং AB = DC প্রমাণ কর যে, AD = BC, ∠CAD = ∠ACB এবং ∠ADC = ∠ABC
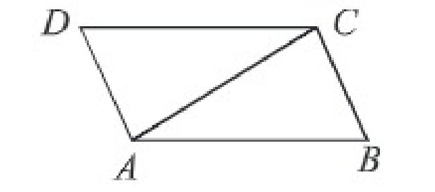
৪। প্রমাণ কর যে, সমদ্বিবাহু ত্রিভুজের সমান বাহু বাদে অপর বাহু উভয়দিকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ দুটি পরস্পর সমান।
৫। চিত্রে, AD = AE, BD = CE এবং ∠AEC = ∠ADB প্রমাণ কর যে, AB = AC
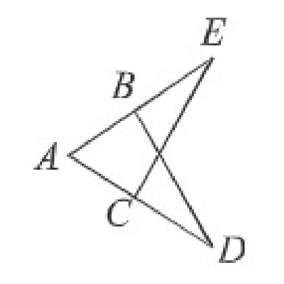
৬। চিত্রে, ∆ABC এবং ∆DBC দুটি সমদ্বিবাহু ত্রিভুজ। প্রমাণ কর যে, ∆ABD = AACD
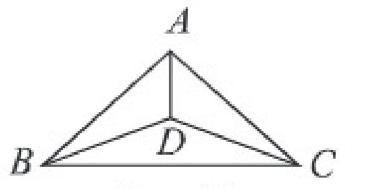
৭। প্রমাণ কর যে, সমদ্বিবাহু ত্রিভুজের ভূমির প্রান্তবিন্দু থেকে বিপরীত বাহুদ্বয়ের উপর অঙ্কিত মধ্যমাদ্বয় সমান।
৮। প্রমাণ কর যে, সমবাহু ত্রিভুজের কোণগুলো পরস্পর সমান।
উপপাদ্য ৩ (বাহু-বাহু-বাহু উপপাদ্য)
যদি একটি ত্রিভুজের তিন বাহু যথাক্রমে অপর একটি ত্রিভুজের তিন বাহুর সমান হয়, তবে ত্রিভুজ দুটি সর্বসম হবে।
বিশেষ নির্বচন: মনে করি, ∆ABC এবং ∆DEF এ AB = DE, AC = DF এবং BC = EF, প্রমাণ করতে হবে যে, ∆ABC ≅ ∆DEF
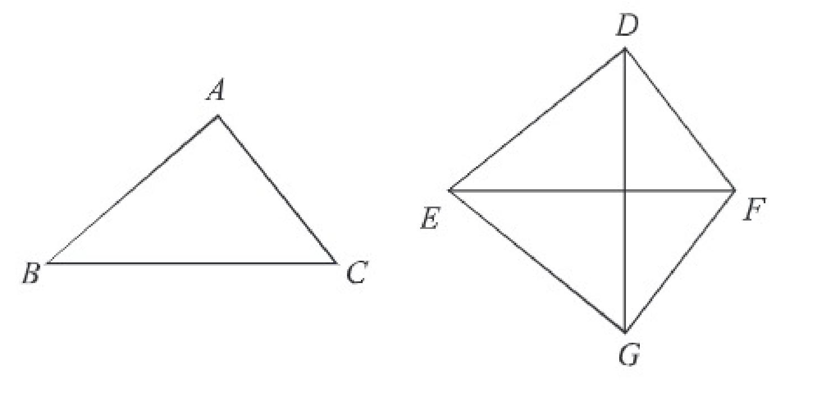
প্রমাণ: মনে করি, BC এবং EF বাহু যথাক্রমে ∆ABC এবং ∆DEF এর বৃহত্তম বাহুদ্বয়।
এখন ∆ABC কে ∆DEF এর উপর এমনভাবে স্থাপন করি, যেন B বিন্দু E বিন্দুর উপর ও BC বাহু EF বাহু বরাবর এবং EF রেখার যে পাশে D বিন্দু আছে, A বিন্দু এর বিপরীত পাশে পড়ে। মনে করি, G বিন্দু A বিন্দুর নতুন অবস্থান।
যেহেতু BC = EF, Cবিন্দু F বিন্দুর উপর পড়বে। সুতরাং ∆GEF হবে ∆ABC এর নতুন অবস্থান। অর্থাৎ, EG = BA, FG=CA ও ∠EGF = ∠BAC D, G যোগ করি।
| ধাপ | যথার্থতা |
| (১) ∆EGD এ EG = ED [কারণ EG = BA = ED] অতএব, ∠EDG = ∠EGD | [ত্রিভুজের সমান বাহুদ্বয়ের বিপরীত কোণ পরস্পর সমান] |
| (২) ∆FGD এ FG = FD অতএব, ∠FDG = ∠FGD | [ত্রিভুজের সমান বাহুদ্বয়ের বিপরীত কোণদ্বয় পরস্পর সমান। |
(৩) সুতরাং, ∠EDG + ∠FDG = ∠EGD + ∠FGD বা, ∠EDF = ∠EGF অর্থাৎ, ∠BAC = ∠EDF ∴∆ABC = ∆DEF (প্রমাণিত)। | [বাহু-কোণ-বাহু উপপাদ্য] |
উপপাদ্য ৪ (কোণ-বাহু-কোণ উপপাদ্য)
যদি একটি ত্রিভুজের দুটি কোণ ও কোণ সংলগ্ন বাহু যথাক্রমে অপর একটি ত্রিভুজের দুটি কোণ ও কোণ সংলগ্ন বাহুর সমান হয়, তবে ত্রিভুজ দুটি সর্বসম হবে।
বিশেষ নির্বচন: মনে করি, ∆ABC = ∆DEF -এ ∠B∠E, ∠C = ∠F এবং কোণ সংলগ্ন BC বাহু = অনুরূপ EF বাহু।

প্রমাণ করতে হবে যে, ∆ABC = ∆DEF
প্রমাণ
| ধাপ | যথার্থতা |
(১) ∆ABC কে ADEF এর উপর এমনভাবে স্থাপন করি যেন, B বিন্দু E বিন্দুর উপর ও BC বাহু EF বাহু বরাবর এবং EF রেখার যে পাশে D আছে বিন্দু A বিন্দু যেন ঐপাশে পড়ে। যেহেতু BC = EF, অতএব C বিন্দু F বিন্দুর উপর অবশ্যই পড়বে। | [ বাহুর সর্বসমতা] |
| (২) আবার, ∠B = ∠E বলে, BA বাহু ED বাহু বরাবর পড়বে এবং ∠C=∠F বলে, CA বাহু FD বাহু বরাবর পড়বে। | |
(৩)∴ BA এবং CA বাহুর সাধারণ বিন্দু A, ED ও FD বাহুর সাধারণ বিন্দু D এর উপর পড়বে। অর্থাৎ, ∆ABC, ∆DEF এর উপর সমাপতিত হবে। ∴∆ABC ≅ ∆DEF (প্রমাণিত)। | [ কোণের সর্বসমতা] |
অনুসিদ্ধান্ত: একটি ত্রিভুজের একটি বাহু ও দুটি কোণ যথাক্রমে অপর একটি ত্রিভুজের একটি বাহু ও দুটি কোণের সমান হলে ত্রিভুজ দুটি সর্বসম।
কাজ 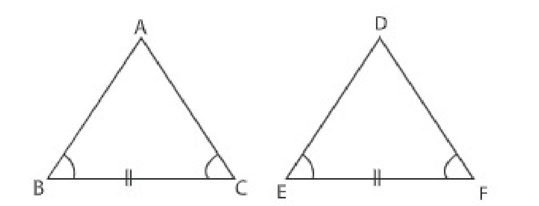 ∆ ABC ও ∆DEF এ BC=EF এবং ∠B=∠E ও ∠C=∠F হলে দেখাও যে, △ ABC ≅ ∆DEF ইঙ্গিত: ∠A+B+C= ∠D+∠E+∠F = ২ সমকোণ হবে। ∴ ∠B=∠E, ∠C=∠F, হলে ∠A=∠D হবে। অতঃপর উপপাদ্য 8 প্রয়োগ কর। |
উদাহরণ ১। প্রমাণ কর যে, কোনো ত্রিভুজের শিরঃকোণের সমদ্বিখণ্ডক যদি ভূমির উপর লম্ব হয়, তবে ত্রিভুজটি সমদ্বিবাহু।
বিশেষ নির্বচন: চিত্রে, ∆ABC এর শিরঃকোণ A-এর সমদ্বিখণ্ডক AD যা ভূমি BC এর D বিন্দুতে লম্ব। প্রমাণ করতে হবে যে, AB = AC
প্রমাণ: ∆ABD এবং ∆ACD এ ∠BAD = ∠CAD [∵AD, ∠BAC এর সমদ্বিখণ্ডক]
∠ADB = ∠ADC [: AD, BC এর উপর লম্ব]
এবং AD সাধারণ বাহু।
সুতরাং ∆ABD ≅ ∆ACD [কোণ বাহু কোণ উপপাদ্য। এতএব, AB = AC [প্রমাণিত]

উপপাদ্য ৫ (সমকোণী অতিভুজ-বাহু উপপাদ্য)
দুটি সমকোণী ত্রিভুজের অতিভুজদ্বয় সমান হলে এবং একটির এক বাহু অপরটির অপর এক বাহুর সমান হলে, ত্রিভুজদ্বয় সর্বসম হবে।

বিশেষ নির্বচন: মনে করি, ABCও DEF সমকোণী ত্রিভুজদ্বয়ে অতিভুজ AC =অতিভুজ DF এবং AB = DE প্রমাণ করতে হবে যে, ∆ABC ≅ ∆DEF
| ধাপ | যথার্থতা |
| (১) ∆ABC কে △DEF এর উপর এমনভাবে স্থাপন করি যেন, B বিন্দু E বিন্দুর উপর, BA বাহু ED বাহু বরাবর এবং C বিন্দু DE এর যে পাশে F বিন্দু আছে এর বিপরীত পাশে পড়ে। ধরি, C বিন্দুর নতুন অবস্থান G। | [ত্রিভুজের দুই বাহু সমান হলে তাদের বিপরীত কোণ দুটি পরস্পর সমান] |
| (২) যেহেতু AB=DE, A বিন্দু D বিন্দুর উপর পড়বে। ফলে △ DEG হবে ∆ABC এর নতুন অবস্থান অর্থাৎ DG AC, ∠G=∠C ∠DEG= ∠B = 1 সমকোণ। | |
(৩) যেহেতু ∠DEF+∠DEG = 1 সমকোণ + 1 সমকোণ = 2 সমকোণ = 1 সরলকোণ, GEF একটি সরলরেখা। সুতরাং △ DGF একটি সমদ্বিবাহু ত্রিভুজ। যার DG=DF ∴ ∠FZG=∠C | [কোণ-বাহু-কোণ উপপাদ্য |
| (৪) এখন △ ABC ও △DEF এর ∠B = ∠E [প্রত্যেকে ১ সমকোণ। ∠C = ∠F এবং AB = অনুরূপ DE সুতরাং △ ABC ≅ △DEF (প্রমাণিত) |
Read more






