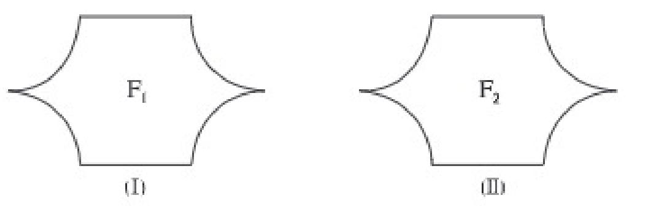
নিচের সমতলীয় চিত্র দুটি দেখতে একই আকৃতি ও আকারের। চিত্র দুটি সর্বসম কিনা নিশ্চিত হওয়ার জন্য উপরিপাতন পদ্ধতি গ্রহণ করা যায়। এ পদ্ধতিতে প্রথম চিত্রের একটি অনুরূপ কপি করে দ্বিতীয়টির উপর রাখি। যদি চিত্রগুলো পরস্পরকে সম্পূর্ণরূপে আবৃত করে, তবে এরা সর্বসম। চিত্র F1, চিত্র F2 এর সর্বসম হলে আমরা F1 ≅ F2 দ্বারা প্রকাশ করি।
দুটি রেখাংশ কখন সর্বসম হবে? চিত্রে দুই জোড়া রেখাংশ আঁকা হয়েছে। উপরিপাতন পদ্ধতিতে AB এর অনুরূপ কপি CD এর উপর রেখে দেখি যে, AB রেখাংশ CD রেখাংশকে ঢেকে দিয়েছে এবং A ও B বিন্দু যথাক্রমে C'ওD বিন্দুর উপর পতিত হয়েছে। সুতরাং রেখাংশ দুটি সর্বসম। একই কাজ দ্বিতীয় জোড়া সরলরেখার জন্য করে দেখি যে, রেখাংশ দুটি সর্বসম নয়। লক্ষ করি, কেবল প্রথম জোড়া রেখাংশের দৈর্ঘ্য সমান।

| দুটি রেখাংশের দৈর্ঘ্য সমান হলে রেখাংশ দুটি সর্বসম। আবার বিপরীতভাবে, দুটি রেখাংশ সর্বসম হলে এদের দৈর্ঘ্য সমান। |
দুইটি কোণ কখন সর্বসম হবে? চিত্রে 40° দুইটি কোণ আঁকা হয়েছে। উপরিপাতন পদ্ধতি গ্রহণ করে প্রথম চিত্রের একটি অনুরূপ কপি করে দ্বিতীয়টির উপর রাখি। B বিন্দু Q বিন্দুর উপর এবং BA রশ্মি QP রশ্মির ওপর পতিত হয়েছে। লক্ষ করি, কোণ দুটির পরিমাপ সমান বলে BC রশ্মি QR রশ্মির উপর পতিত হয়েছে। অর্থাৎ ∠ABC ≅ ∠PQR
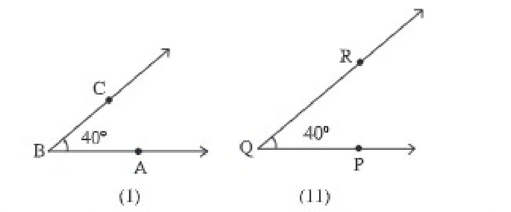
| দুটি কোণের পরিমাপ সমান হলে কোণ দুটি সর্বসম। আবার বিপরীতভাবে, দুটি কোণ সর্বসম হলে এদের পরিমাপও সমান। |
Read more






