Summary
নিম্নলিখিত প্রমাণগুলো সংক্ষেপে তুলে ধরা হলো:
-
∆ABC এ AB = AC হলে, O বিন্দুতে OB = OC হলে ∠AOB = ∠AOC প্রমাণ করা হবে।
-
∆ABC এর AB ও AC বাহুতে D ও E বিন্দুতে BD = CE এবং BE = CD হলে ∠ABC = ∠ACB প্রমাণ করতে হবে।
-
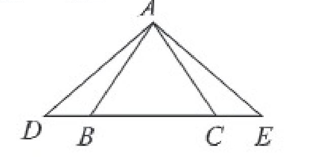
চিত্রে AB = AC, BD = DC এবং BE = CF হলে ∠EDB = ∠FDC প্রমাণ করা হবে।
-
চিত্রে AB = AC এবং ∠BAD = ∠CAe হলে AD = AE প্রমাণ করনোর প্রয়োজন।
-
ABCD চতুর্ভুজে AC সমদ্বিখণ্ডক হলে ∠B = ∠D প্রমাণ করতে হবে।
-
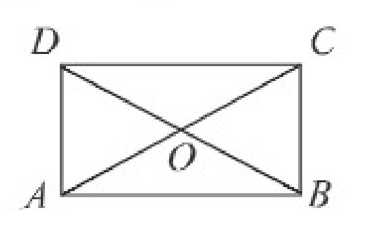
চিত্রে AB এবং CD সমান্তরাল হলে AD = BC প্রমাণের প্রয়োজন।
-
সমদ্বিবাহু ত্রিভুজের ভূমির প্রান্তবিন্দু থেকে বিপরীত বাহুর উপর অঙ্কিত লম্বদ্বয় পরস্পর সমান।
-
যদি ত্রিভুজের ভূমির প্রান্ত বিন্দুদ্বয় থেকে বিপরীত বাহুর উপর অঙ্কিত লম্বদ্বয় সমান হয়, তবে ত্রিভুজটি সমদ্বিবাহু।
-
AB = AD এবং ∠B = ∠D = একই সমকোণ হলে ∆ABC ≅ ∆ADC প্রমাণ করা হবে।
১। ∆ABC এ AB = AC এবং O, ABC এর অভ্যন্তরে এমন একটি বিন্দু যেন OB = OC হয় প্রমাণ কর যে, ∠AOB = ∠AOC
২। ∆ABC এর AB ও AC বাহুতে যথাক্রমে DওE এমন দুটি বিন্দু যেন BD = CE এবং BE = CD প্রমাণ কর যে, ∠ABC = ∠ACB
৩। চিত্রে, AB = AC, BD = DC এবং BE = CF | প্রমাণ কর যে, ∠EDB = ∠FDC

৪। চিত্রে, AB = AC এবং ∠ BAD = ∠ CAE । প্রমাণ কর যে, AD = AE
৫। ABCD চতুর্ভুজে AC, ∠ BAD এবং ∠ BCD এর সমদ্বিখণ্ডক। প্রমাণ কর যে, ∠ B = ∠ D
৬। চিত্রে, AB এবং CD পরস্পর সমান ও সমান্তরাল এবং AC ও BD কর্ণ দুটি বিন্দুতে ছেদ করেছে। প্রমাণ কর যে, AD = BC
৭। প্রমাণ কর যে, সমদ্বিবাহু ত্রিভুজের ভূমির প্রান্তবিন্দুদ্বয় থেকে বিপরীত বাহুর উপর অঙ্কিত লম্বদ্বয় পরস্পর সমান।
৮। প্রমাণ কর যে, কোনো ত্রিভুজের ভূমির প্রান্ত বিন্দুদ্বয় থেকে বিপরীত বাহুর উপর অঙ্কিত লম্বদ্বয় যদি সমান হয়, তবে ত্রিভুজটি সমদ্বিবাহু।
৯। ABCD চতুর্ভুজের AB = AD এবং ∠B = ∠D = এক সমকোণ। প্রমাণ কর যে, ∆ABC ≅ AADC
Read more






