সংখ্যারেখার মূলদ সংখ্যা
নিচের সংখ্যারেখাটি লক্ষ করি:

উপরের সংখ্যারেখাটিতে গাঢ় চিহ্নিত বৃত্তটি ২ এর অবস্থান নির্দেশ করে।
আবার,

উপরের সংখ্যারেখাটিতে গাঢ় চিহ্নিত বৃত্তটির অবস্থান ১ ও ২ এর মাঝে। গাঢ় চিহ্নিত অংশটুকু ৪ ভাগের বা নির্দেশ করে।
সংখ্যারেখায় অমূলদ সংখ্যা
একটি অমূলদ সংখ্যা যেখানে __________ = ১.৭ (আসন্ন মান)।
এবার সংখ্যারেখায় ১ ও ২ এর মাঝের অংশকে সমান ১০ অংশে ভাগ করে সপ্তম অংশটি গাঢ় করি যার আসন্ন মান ১.৭ তথা নির্দেশ করে।

অতএব গাঢ় চিহ্নিত বৃত্তটি সংখ্যারেখায় অবস্থান।
| কাজ: ১। সংখ্যা রেখায় এবং সংখ্যাগুলো প্রকাশ কর। |
উদাহরণ ৯। কোনো বাগানে ১২৯৬টি আমগাছ আছে। বাগানের দৈর্ঘ্য ও প্রস্থের উভয় দিকের প্রত্যেক সারিতে সমান সংখ্যক আমগাছ থাকলে প্রত্যেক সারিতে গাছের সংখ্যা নির্ণয় কর।
সমাধান: বাগানের দৈর্ঘ্য ও প্রস্থের উভয় দিকের প্রত্যেক সারিতে সমান সংখ্যক আমগাছ আছে।
প্রত্যেক সারিতে আমগাছের সংখ্যা হবে ১২৯৬ এর বর্গমূল।
এখন,
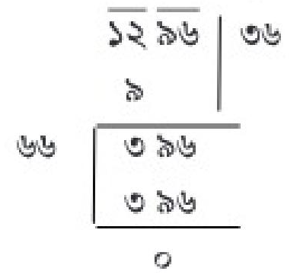
নির্ণেয় আমগাছের সংখ্যা ৩৬ টি।
উদাহরণ ১০। একটি স্কাউট দলকে ৯, ১০, এবং ১২ সারিতে সাজানো যায়। আবার তাদের বর্গাকারেও সাজানো যায়। ঐ স্কাউট দলে কমপক্ষে কতজন স্কাউট রয়েছে?
সমাধান: স্কাউট দলকে ৯, ১০ এবং ১২ সারিতে সাজানো যায়। ফলে স্কাউট এর সংখ্যা ৯, ১০ এবং ১২ দ্বারা বিভাজ্য। এরূপ ক্ষুদ্রতম সংখ্যা হবে ৯, ১০ এবং ১২ এর ল.সা.গু.।
এখানে,

৯, ১০ এবং ১২ এর ল.সা.গু.
প্রাপ্ত ল.সা.গু. কে বর্গাকারে সাজানো যায় না।
কে বর্গসংখ্যা করতে হলে কমপক্ষে ৫ দ্বারা গুণ করতে হবে।
৯, ১০ এবং ১২ সারিতে এবং বর্গাকারে সাজানোর জন্য স্কাউট এর সংখ্যা প্রয়োজন
নির্ণেয় স্কাউট এর সংখ্যা ৯০০।
উদাহরণ ১১। ২১৯৫২ এবং ৫৬০৫ দুটি সংখ্যা।
(ক) প্রথম সংখ্যাটি কী পূর্ণবর্গ সংখ্যা যুক্তি দাও।
(খ) প্রথম সংখ্যাটি যদি পূর্ণবর্গ না হয়, তবে একে কোন ক্ষুদ্রতম সংখ্যা দ্বারা ভাগ করলে পূর্ণবর্গ সংখ্যা হবে।
(গ) দ্বিতীয় সংখ্যাটির সাথে কোন ক্ষুদ্রতম সংখ্যা যোগ করলে, যোগফল একটি পূর্ণবর্গ সংখ্যা হবে।
সমাধান:
(ক) যে সংখ্যার সর্ব ডানদিকের অঙ্ক অর্থাৎ একক স্থানীয় অঙ্ক ২ বা ৩ বা ৭ বা ৮ তা পূর্ণবর্গ নয়। যেহেতু ২১৯৫২ সংখ্যাটির একক স্থানীয় অঙ্কটি ২ সেহেতু সংখ্যাটি পূর্ণবর্গ নয়।
(খ)
এখানে

সুতরাং
২১৯৫২ সংখ্যাটি পূর্ণবর্গ নয়। সংখ্যাটিকে ৭ দ্বারা ভাগ করলে প্রাপ্ত সংখ্যাটি পূর্ণবর্গ হবে।
উত্তর: ৭
গ. এখানে,

যেহেতু সংখ্যাটির বর্গমূল নির্ণয় করার সময় ভাগশেষ ১২৯ আছে সেহেতু সংখ্যাটি পূর্ণবর্গ নয়। ৫৬০৫ এর সাথে কোনো একটি ক্ষুদ্রতম সংখ্যা যোগ করলে যোগফল পূর্ণবর্গ হবে।
বর্গমূল হবে (৭৪+১)=৭৫
৭৫ এর বর্গ = (৭৫ ৭৫)=৫৬২৫
সুতরাং, নির্ণেয় ক্ষুদ্রতম সংখ্যাটি=৫৬২৫-৫৬০৫=২০
উত্তর: ২০
Read more






