কোনো ঘটনা, কোনো রাশি বা কোনো অপেক্ষকের (function) বা কোনো কিছুর যদি বার বার পুনরাবৃত্তি ঘটে তবে তাকে আমরা বলি পর্যাবৃত্তিক ঘটনা বা রাশি বা অপেক্ষক। যেমন, প্রতি বছর ২৬ মার্চ আমরা স্বাধীনতা দিবস পালন করি, প্রতি বছর ১ বৈশাখ আমাদের বাংলা নববর্ষ। প্রতি সপ্তাহে শুক্রবার সরকারি ছুটি থাকে, ঘড়ির একটা কাঁটা নির্দিষ্ট সময় পরপর একটি নির্দিষ্ট দাগ অতিক্রম করে, সাইন (sine) বা কোসাইন (cosine) ফাংশনগুলো 360° পরপর একই মান গ্রহণ করে। পর্যাবৃত্তি দু'রকমের হতে পারে স্থানিক পর্যাবৃত্তি এবং কালিক পর্যাবৃত্তি।
স্থানিক পর্যাবৃত্তি (Spatial periodicity)
সংজ্ঞা : কোনো বস্তুর গতি যদি এমনভাবে পুনরাবৃত্তি হয় যে নির্দিষ্ট সময় পরপর কোনো নির্দিষ্ট বিন্দুকে একই দিক থেকে অতিক্রম করে তবে তাকে বলে স্থানিক পর্যাবৃত্তি। ঘড়ির কোনো কাঁটার গতি, সূর্যের চারপাশে গ্রহগুলোর গতি, একটি উল্লম্ব স্প্রিং এর তরঙ্গের উপরিস্থ কোনো কণার গতি ইত্যাদি স্থানিক পর্যাবৃত্তির উদাহরণ ।
কালিক পর্যাবৃত্তি (Temporal periodicity)
সংজ্ঞা : কোনো রাশি বা ফাংশনের মান যদি এমন হয় যে নির্দিষ্ট সময় পরপর সেটি একই মান গ্রহণ করে যেমন, ১৬ ডিসেম্বর আমাদের জাতীয় বিজয় দিবস, প্রতি এক বছর পর পর এর পুনরাবৃত্তি ঘটে; আমরা বাড়িঘরে যে তবে তাকে বলে কালিক পর্যাবৃত্তি।
তড়িৎ প্রবাহ ব্যবহার করি সেটি হচ্ছে পর্যাবৃত্ত বা দিক পরিবর্তী প্রবাহ (alternating current বা AC)। এ প্রবাহ আমাদের দেশে প্রতি 0.02s পরপর একই মান গ্রহণ করে। এ অধ্যায়ে এবং এ বই-এর অন্যত্র অন্যভাবে উল্লেখ না করলে পর্যাবৃত্তি বলতেই আমরা স্থানিক পর্যাবৃত্তিকে বোঝাবো।
# বহুনির্বাচনী প্রশ্ন
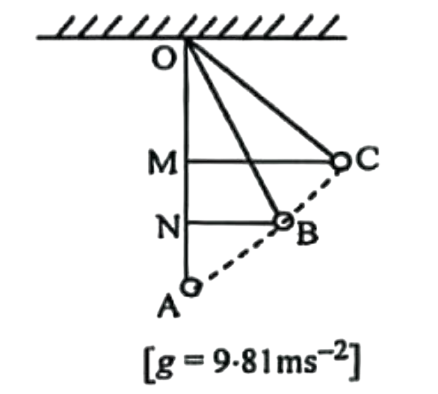
চিত্রের 20gm ভরের একটি বব একটি সুতা দিয়ে ঝুলানো আছে। যেখানে, OA = 1m, AM = 20 cm
সংজ্ঞা : কোনো গতিশীল বস্তু কণার গতি যদি এমন হয় যে, এটি এর গতিপথে কোনো নির্দিষ্ট বিন্দুকে নির্দিষ্ট সময় পরপর একই দিক থেকে অতিক্রম করে, তাহলে সেই গতিকে পর্যাবৃত্ত গতি বলে।
এ গতিপথ বৃত্তাকার, উপবৃত্তাকার, সরল রৈখিক বা আরো জটিল হতে পারে। ঘড়ির কাঁটার গতি, সূর্যের চারদিকে পৃথিবীর গতি, বাষ্প বা পেট্রোল ইঞ্জিনের সিলিন্ডারের মধ্যে পিস্টনের গতি পর্যাবৃত্ত গতি ।
পর্যায়কাল
সংজ্ঞা : পর্যাবৃত্ত গতিসম্পন্ন কোনো কণা যে নির্দিষ্ট সময় পরপর কোনো নির্দিষ্ট বিন্দুকে নির্দিষ্ট দিক দিয়ে অতিক্রম করে সেই সময়কে পর্যায়কাল (T) বলে।
স্পন্দন গতি বা দোলন গতি
কোনো অগ্রপশ্চাৎ পর্যাবৃত্ত গতিকে দোলন গতি বা স্পন্দন গতি বলে ।
সংজ্ঞা : পর্যাবৃত্ত গতি সম্পন্ন কোনো বস্তু যদি পর্যায়কালের অর্ধেক সময় কোনো নির্দিষ্ট দিকে এবং বাকি অর্ধেক সময় একই পথে তার বিপরীত দিকে চলে তবে এর গতিকে স্পন্দন গতি বলে।
উদাহরণ : স্পন্দন গতির উদাহরণ হচ্ছে সরল দোলকের গতি, কম্পনশীল সুরশলাকা ও গীটারের তারের গতি। কঠিন বস্তুতে পরমাণু স্পন্দিত হয়। বাতাসের মধ্য দিয়ে শব্দ তরঙ্গ সঞ্চালনের সময় বাতাসের অণুগুলো স্পন্দিত হয় ।
৮.৩। সরল দোলন গতি বা সরল দোল গতি বা সরল ছন্দিত গতি
Simple Harmonic Motion
আমরা আগেই দেখেছি সরলরৈখিক গতির ক্ষেত্রে ত্বরণ মানে ও দিকে ধ্রুব থাকে, বৃত্তাকার গতির ক্ষেত্রে ত্বরণ (কেন্দ্রমুখী ত্বরণ) মানে ধ্রুব থাকলেও এর দিক পরিবর্তিত হয়। স্পন্দন গতির ক্ষেত্রে ত্বরণ পর্যায়বৃত্তভাবে মানে ও দিকে পরিবর্তিত হয়। স্পন্দন গতির ক্ষেত্রে ত্বরণ সরণের ওপর নির্ভর করে। ত্বরণ ও সরণের মানের মধ্যে সবচেয়ে সরল সম্পর্ক হতে পারে কোনো কণার ত্বরণ a, তার সরণ x এর সমানুপাতিক। এ জাতীয় সম্পর্ক যে স্পন্দন গতিতে বজায় থাকে তাকে বলা হয় সরল ছন্দিত স্পন্দন বা সরল দোলন গতি এবং একে নিম্নোক্তভাবে সংজ্ঞায়িত করা হয়।
সংজ্ঞা : যদি কোনো বস্তুর ত্বরণ একটি নির্দিষ্ট বিন্দু থেকে এর সরণের সমানুপাতিক এবং সর্বদা ঐ বিন্দু অভিমুখী হয়, তাহলে বস্তুর এই গতিকে সরল দোলন গতি বলে।
সুতরাং সরল ছন্দিত স্পন্দনের ক্ষেত্রে ত্বরণ a এবং সরণ x এর মধ্যে সম্পর্ক হলো,
.. .. .. (8.1)
এই ধ্রুবক k কে বলা হয় বল ধ্রুবক।
যেহেতু বল ত্বরণের সমানুপাতিক, সুতরাং সরল দোলন গতির ক্ষেত্রে আমরা বলতে পারি বলও সরণের সমানুপাতিক,
এখানে ' বা k হচ্ছে ধনাত্মক ধ্রুবক। (8.1) এবং (82) সমীকরণে ঋণাত্মক চিহ্ন নির্দেশ করে যদিও সরণ বেশি হলে ত্বরণ ও বল বেশি হয় কিন্তু তাদের দিক সর্বদা সরণের দিকের বিপরীত দিকে অর্থাৎ সাম্যাবস্থানের দিকে। এ বল একটি প্রত্যায়নী বল। যে বল সরল দোলন গতির ক্ষেত্রে সর্বদা সাম্যাবস্থানের দিকে ক্রিয়া করে সাম্যাবস্থানের দিকে ফিরিয়ে আনে তাকে প্রত্যায়নী বল বলা হয় যেমন-স্প্রিং বল, স্থিতিস্থাপক বল ইত্যাদি।
উদাহরণ : সরল দোলন গতির কয়েকটি উদাহরণ হলো কম্পমান সুরশলাকার গতি, স্বল্প বিস্তারে কোনো সরল দোলকের গতি, কোনো স্প্রিং-এর এক প্রান্ত দৃঢ় অবস্থানে আটকে অপর প্রান্তে একটি ভারী বস্তু ঝুঁলিয়ে টেনে ছেড়ে দিলে তার গতি প্রভৃতি।
সরল দোলন গতির ক্ষেত্রে বলের বৈশিষ্ট্য
১। এটি একটি পর্যাবৃত্ত বল।
২। এটি একটি স্পন্দনশীল বল ।
৩। যেকোনো সময় বলের মান সাম্যাবস্থান থেকে সরণের মানের সমানুপাতিক ।
৪ । বল সর্বদা একটি নির্দিষ্ট বিন্দু অভিমুখী ।
সরল দোলন গতি সংক্রান্ত কয়েকটি রাশি
পূর্ণ স্পন্দন : সরল দোলন গতির ক্ষেত্রে একটি সম্পূর্ণ অগ্র-পশ্চাৎ গতিকে পূর্ণ স্পন্দন বা দোলন বলে।
পর্যায়কাল: একটি পূর্ণ দোলন সম্পন্ন হতে যে সময় লাগে, তাকে পর্যায়কাল T বলে। কম্পাঙ্ক : একক সময়ে যতগুলো পূর্ণ দোলন হয় তাকে কম্পাঙ্ক f বলে।
বিস্তার : সরল দোলন গতিশীল কোনো কণা এর সাম্যাবস্থান বা মধ্যাবস্থান থেকে যেকোনো একদিকে যে সর্বোচ্চ দূরত্ব অতিক্রম করে তাকে তার বিস্তার বলে।
দশা : সরল দোলন গতিশীল কোনো কণার দশা বলতে ঐ কণার যেকোনো মুহূর্তে গতির সম্যক অবস্থা অর্থাৎ কণাটির সরণ, বেগ, ত্বরণ, বল ইত্যাদি বোঝায়।
সরল দোলন গতি সংক্রান্ত কয়েকটি রাশি
পূর্ণ স্পন্দন : সরল দোলন গতির ক্ষেত্রে একটি সম্পূর্ণ অগ্র-পশ্চাৎ গতিকে পূর্ণ স্পন্দন বা দোলন বলে।
পর্যায়কাল: একটি পূর্ণ দোলন সম্পন্ন হতে যে সময় লাগে, তাকে পর্যায়কাল T বলে। কম্পাঙ্ক : একক সময়ে যতগুলো পূর্ণ দোলন হয় তাকে কম্পাঙ্ক f বলে।
বিস্তার : সরল দোলন গতিশীল কোনো কণা এর সাম্যাবস্থান বা মধ্যাবস্থান থেকে যেকোনো একদিকে যে সর্বোচ্চ দূরত্ব অতিক্রম করে তাকে তার বিস্তার বলে।
দশা : সরল দোলন গতিশীল কোনো কণার দশা বলতে ঐ কণার যেকোনো মুহূর্তে গতির সম্যক অবস্থা অর্থাৎ কণাটির সরণ, বেগ, ত্বরণ, বল ইত্যাদি বোঝায়।
৮.৪। সরল দোলন গতির অন্তরক বা ব্যবকলনীয় সমীকরণ
Differential Equation of Simple Harmonic Motion
সরল দোলন গতির সংজ্ঞা থেকে আমরা জানি, বল সরণের সমানুপাতিক এবং বিপরীতমুখী। কোনো কণার উপর ক্রিয়াশীল বল F এবং সরণ x হলে সরল দোলন গতির ক্ষেত্রে,
এ ধ্রুবক k কে বলা হয় বল ধ্রুবক। নিউটনের দ্বিতীয় সূত্র থেকে বস্তুর ভর m এবং ত্বরণ a হলে, F = ma
:- ma =- Kx
কিন্তু ত্বরণ
:-
…(8.3)
আমরা যদি 2লিখি, তাহলে এ সমীকরণ দাঁড়ায়,
.. .. (8.4)
এ সমীকরণে অন্তরক (derivative) সংশ্লিষ্ট, কাজেই এ সমীকরণটি একটি অন্তরক বা ব্যবকলনী সমীকরণ। এ সমীকরণ থেকে সরল দোলন গতি সম্পন্ন কোনো কণার সরণ x কীভাবে সময় এর উপর নির্ভর করে তা জানা যায়। কোনো কণার সরণ x কীভাবে সময়। এর উপর নির্ভর করে তা জানার অর্থই হচ্ছে কণাটির গতি সম্পর্কে জানা। যেহেতু (8.4) সমীকরণ সমাধান করলে সময়ের সাথে সরণের সম্পর্ক তথা গতি সম্পর্কে জানা যায়, তাই এ সমীকরণকে সরল দোলন গতির অন্তরক সমীকরণ বলা হয়। এ সমীকরণের দুটি উল্লেখযোগ্য সাধারণ সমাধান হচ্ছে
(i) এটি একটি বিশেষ ধরনের ছদিত বা দোলনগতিসম্পন্ন কণার উপর সৃষ্ট বল।
(ii) এই গতির ক্ষেত্রে কণার ত্বরণ এবং এর উপর ক্রিয়াশীল বল-এর মান কণার সরণের সমানুপাতিক।
(iii) ত্বরণের এবং কণার উপর ক্রিয়াশীল বলের অভিমুখ সব সময় সাম্যাবস্থানের দিকে হয়, অর্থাৎ কণার সরণের বিপরীত দিকে হয়।
(iv) এই ধরনের গতির বলের গতিপথ স্যালরৈখিক হয়। কোনো দোলনরত কণার ত্বরণ সাম্যাবস্থান থেকে এর দূরত্বের সমানুপাতিক ও সব সময় সাম্যাবস্থানের অভিমুখী হলে ঐ কণার গতিকে সরল ছন্দিত গতি বলে।
স্পষ্টত সব পর্যাবৃত্ত গতির এই বৈশিষ্ট্যগুলি থাকে না। তাই সরল ছন্দিত গতি মাত্রই পর্যাবৃত্ত গতি হলেও সব পর্যাবৃত্ত গতি সরল ছন্দিত গতি বা সরল দোলগতি নয়।
সরল দোলন গতি সংক্রান্ত বিভিন্ন রাশি
Quantities Related to Simple Harmonic Motion
পূর্বের অনুচ্ছেদে আমরা দেখেছি সরল দোলন গতির অন্তরক সমীকরণের একটি সমাধান তথা সরল দোলন গতি সম্পন্ন
কণার গতির সমীকরণ হচ্ছে, (সমীকরণ 8.7)
এখন আমরা এ সমীকরণের বিভিন্ন রাশির ভৌত তাৎপর্য নিয়ে আলোচনা করব।
পর্যায়কাল, T
সরল দোলন গতি সম্পন্ন কোনো কণার একটি পূর্ণ দোলনসম্পন্ন হতে যে সময় লাগে তাকে তার পর্যায়কাল T বলে ( 87 ) সমীকরণে সময় কে পরিমাণ বৃদ্ধি করা হলে সরণ হয়।
দেখা যাচ্ছে যে, সময় পর সরণের মান একই হচ্ছে অর্থাৎ সময় পর পর রাশিটির পুনরাবৃত্তি ঘটছে। সুতরাং হচ্ছে সরল দোলন গতির পর্যায়কাল T।
:- T =
পর্যায়কাল ও বল ধ্রুবকের সম্পর্ক
আমরা জানি, = । সুতরাং T = সমীকরণ দাঁড়ায়,
এ সমীকরণ থেকে দেখা যায় যে, সরল দোলন গতির পর্যায়কাল স্পন্দনশীল কণাটির ভর m এবং বল ধ্রুবক k এর সাথে সম্পর্কিত। যেহেতু কোনো কণার ভর m নির্দিষ্ট
:-
অর্থাৎ সরল দোলন গতি সম্পন্ন কোনো কণার পর্যায়কাল বল ধ্রুবকের বর্গমূলের ব্যস্তানুপাতিক।
কম্পাঙ্ক, f
কোনো সরল দোলন গতি সম্পন্ন কণা একক সময়ে যে কয়টি পূর্ণ দোলন বা কম্পন সম্পন্ন করে তাকে তার কম্পাঙ্ক f বলে।
কৌণিক কম্পাঙ্ক,
সরল দোলন গতিসম্পন্ন কোনো কণা একক সময়ে যে কৌণিক দূরত্ব অতিক্রম করে তাকে কৌণিক কম্পাঙ্ক D বলে। পর্যায়কাল এবং কম্পাঙ্ক যথাক্রমে T এবং f হলে,
বিস্তার, A
(8.7) সমীকরণের ধ্রুবক A এর একটি সরল ভৌত তাৎপর্য আছে। আমরা জানি, sine অপেক্ষকের মান – 1 থেকে +1 পর্যন্ত হতে পারে। কাজেই মধ্যবর্তী সাম্যাবস্থান ( x = 0 ) থেকে সরণ x এর সর্বোচ্চ মান হতে পারে । যেহেতু কোনো কণা সাম্যাবস্থান থেকে যেকোনো এক দিকে যে সর্বোচ্চ দূরত্ব অতিক্রম করে তাকে বিস্তার এ বলে, সুতরাং A হচ্ছে সরল দোলন গতির বিস্তার।
দশা,( )
সরল দোলন গতিসম্পন্ন কোনো কণার দশা বলতে ঐ কণার যেকোনো মুহূর্তে গতির সম্যক অবস্থা বোঝায়। কোনো একটি মুহূর্তে গতির সম্যক অবস্থা বলতে ঐ বিশেষ মুহূর্তে বস্তু কণাটির সরণ, বেগ, ত্বরণ, বল ইত্যাদি বোঝায়। (8.7) সমীকরণের ( ) রাশিটি হচ্ছে গতির দশা (Phase)। ধ্রুবক ৪ হলো দশা ধ্রুবক। একই বিস্তার এবং কম্পাঙ্কের কিন্তু ভিন্ন দশার একাধিক গতি হতে পারে।
যেমন, = 0° হলে
বা, x = A sin
সুতরাং 1 = 0 সময়ে x = A অর্থাৎ সরণ হচ্ছে সর্বোচ্চ । এক্ষেত্রে কণাটির গতি শুরু হয় এক প্রান্ত থেকে। অন্য দশা ধ্রুবকের জন্য অন্য আদি সরণ পাওয়া যায়।
কণাটির আদি অবস্থান এবং দ্রুতি দ্বারা সরল দোলন গতির বিস্তার A এবং দশা ধ্রুবক নির্ণীত হয়। এ দুই আদি শর্ত দ্বারা সঠিকভাবে A এবং এর মান নির্ধারিত হয়। একবার গতি শুরু হলে অবশ্য একটি নির্দিষ্ট কম্পাঙ্কের স্পন্দনশীল কণার বিস্তার ও দশা ধ্রুবক ধ্রুব থাকে, যদি না অন্যান্য বল ক্রিয়া করে।
বেগ, V
(8.7) সমীকরণকে সময়ের সাপেক্ষে অন্তরীকরণ করে সরল দোলন গতি সম্পন্ন কণার বেগ পাওয়া যায়।
আমরা জানি সময় সাপেক্ষে সরণের পরিবর্তনের হারকে বেগ বলে। একে সাধারণত v দ্বারা প্রকাশ করা হয়।
... …(8.9)
সমীকরণ (8.1) বেগ ও সরণের মধ্যে সম্পর্ক নির্দেশ করে।
৮.১ চিত্র অনুযায়ী N বিন্দুর গতিপথের মধ্য অবস্থানে তার বেগ সর্বাধিক এবং সরণ বৃদ্ধির সাথে সাথে বেগ কমতে থাকে এবং চরম অবস্থানে B বা D বিন্দুতে এর বেগ শূন্য হবে অর্থাৎ বিস্তারের প্রান্তে বেগ শূন্য হবে। সরল ছন্দিত গতি সম্বন্ধে কণার বেগ-সময় লেখচিত্র একটি cos সদৃশ লেখচিত্র [চিত্র ৮.১ (খ)]।
ত্বরণ (Acceleration) :
আমরা জানি সময় সাপেক্ষে বেগের পরিবর্তনের হারকে ত্বরণ বলে। একে a দ্বারা নির্দেশ করা হয়।
ত্বরণ,
সমীকরণ (8.10) ত্বরণ ও সরণের মধ্যে সম্পর্ক নির্দেশ করে। ঋণ চিহ্ন বুঝায় যে, ত্বরণ ও সরণ পরস্পর বিপরীতমুখী।
৮.১ (খ) চিত্রে N বিন্দুর গতিপথের চরম অবস্থানে ত্বরণ সর্বাধিক এবং মধ্য অবস্থানে ত্বরণ শূন্য হবে। ত্বরণ-সময় লেখচিত্র একটি ঋণাত্মক sin সদৃশ লেখ। ইহা সরল ছন্দিত গতিসম্পন্ন কণার ত্বরণের সমীকরণ নির্দেশ করে।
# বহুনির্বাচনী প্রশ্ন
# বহুনির্বাচনী প্রশ্ন
বৃত্তাকার গতি এক ধরনের সরল দোলন গতি। অর্থাৎ বৃত্তাকার গতি সরল দোলন গতির বৈশিষ্ট্যগুলি মেনে চলে। এখন সরল দোলন গতি এবং বৃত্তাকার গতির মধ্যে সম্পর্ক স্থাপন করতে গিয়ে ৮-৫ চিত্র লক্ষ কর। মনে করি একটি বস্তুকণা A বিন্দু হতে যাত্রা শুরু করে ABCD বৃত্তাকার পথে ঘড়ির কাঁটার বিপরীত দিকে
সমকৌণিক বেগ -এ ঘুরছে [চিত্র ৮-৫(ক)। ধরি বৃত্তের কেন্দ্র এবং A বৃত্তের ব্যাসার্ধ। মনে করি । সময় পর বস্তুকণাটি । অবস্থানে আসল। এখন P বিন্দু হতে বৃত্তের BOD ব্যাসের উপর PN লম্ব অঙ্কন করি। N হবে লম্বটির পাদ বিন্দু।
মনে করি ON =y। চিত্রে OPN ত্রিভুজ থেকে পাওয়া যায়,
y = OP sin = A sin
যেহেতু কণাটি সমকৌণিক বেগে ঘুরছে, সুতরাং
-কে কণাটির দশা কোণ (phase angle) বা সংক্ষেপে দশা বলে।
এখন y = A sin = A sin কণাটি যখন বৃত্তাকার পথে ঘুরতে থাকে তখন ব্যাস BOD-এর উপর কণার পাদবিন্দু N ব্যাস BOD বরাবর স্পন্দিত হতে থাকে।
সুতরাং কণাটির বেগ,
অর্থাৎ কণাটির ত্বরণ এর সরণের সমানুপাতিক। সুতরাং N বিন্দুর গতি সরল ছন্দিত গতি। O হচ্ছে এই ছন্দিত গতির মধ্যবিন্দু বা সাম্যাবস্থান, B ও D ছদিত গতির প্রান্তীয় অবস্থান এবং P উৎপাদনকারী বিন্দু (generating point)। বৃত্তটির নাম নির্দেশক বৃত্ত (reference circle) এবং কণাটির নাম নির্দেশক কণা (reference particle) [চিত্র ৮-৫(ক)]।
লক্ষ করলে দেখা যাবে যে কণাটি বৃত্তাকার পথে যখন ABCDA পথে একবার ঘুরে আসে সেই সময় পাদবিন্দুটি OBODO ব্যাস বরাবর যাত্রা বিন্দু বা আদি বিন্দু থেকে শুরু করে একবার পদ্ম অতিক্রম শেষ করে আদি বিন্দুতে ফিরে আসে। কণাটির বৃত্তাকার পথে একবার ঘুরতে যে সময় লাগে তাই দোগন বা পর্যায়কাল T। ঐ সময় একই পাদবিন্দুও একবার পথ পরিক্রমা শেষ করে।
মূলতত্ত্ব (Theory): সরল দোলকের সাহায্যে কোনো স্থানের অভিকর্ষজ ত্বরণ নির্ণয় করা যায়। এর জন্য সমীকরণটি হলো,
এখানে, T= দোলন কাল L কার্যকর দৈর্ঘ্য এবং g- অভিকর্ষজ ত্বরন।
উপরের সমীকরণের উভয় পার্শ্বকে বর্গ করে পাই,
বা,
π একটি ধ্রুব রাশি ও একটি নির্দিষ্ট মানে খুব। কাজেই ঐ স্থানে L/T2-এর একটি নির্দিষ্ট মান পাওয়া যাবে এবং গড় L/T2-এর মান সমীকরণে বসিয়ে g-এর মান নির্ণয় করা যাবে।
পরীক্ষা:
প্রথনে একটি স্ট্যান্ড হতে হুকের সাহায্যে সুতা খুলিয়ে সুতার হাতে বরকে আটকে সরল দোলক তৈরি করা হয় [চিত্র ৮.৩] এরপর মিটার স্কেলের সাহায্যে একটি সরল দোলকের সুতার দৈর্ঘ্য এবং স্লাইড ক্যালিপার্সের সাহায্যে দোলকের গোলাকার পিন্ডের ব্যাস হতে ব্যাসার্ধ। জেনে দোলকের কার্যকর দৈর্ঘ্য, L = l+r নির্ণয় করা হয়। এরপর পর্যবেক্ষণ স্থানে দোলকটিকে 4° অপেক্ষা কম কৌণিক বিস্তারে দুলতে দিয়ে একটি স্টপ ওয়াচের সাহায্যে তার ১০টি পূর্ণদোলনের সময় কাল নির্ণয় করে 20 দ্বারা ভাগ করে দোলন কাল T =t/20 বের করা হয় এবং দোলনকালের বর্গ নির্ণয় করা হয়। সুতরাং দৈর্ঘ্য I পরিবর্তন করে অনুরূপভাবে বিভিন্ন কার্যকর দৈর্ঘ্যে নোলকের দোলনকাল নির্ণয় করা হয় এবং প্রত্যেক ক্ষেত্রে দোলনকালের বর্ণ বের করা হয়।
(২) পাহাড়ের উচ্চতা নির্ণয়
সরল দোলকের সাহায্যে কোনো পাহাড়ের উচ্চতা অর্থাৎ ভূ-পৃষ্ঠ হতে পাহাড়ের চূড়া বিন্দুর মধ্যবর্তী দূরত্ব নির্ণয় করা যায়। চিত্র[ ৮.৪]। প্রথমে পাহাড়ের পাদদেশে অর্থাৎ ভূ-পৃষ্ঠে সরল দোলকের সাহায্যে অভিকর্ষজ ত্বরণের মান উপরের নিয়মে নির্ণয় করা হয়। মনে করি এই মান -g
এর পর পাহাড়ের চূড়ার অভিকর্ষজ ত্বরণের মান অনুরূপভাবে নির্ণয় করা যায়।
ধরি এই মান = g
হিসাব ও গণনা : নিউটনের মহাকর্ষজ সূত্রানুসারে পাহাড়ের পাদদেশে,
…. (8.11)
এবং পাহাড়ের চূড়ায়,
… (8.12)
এখানে, M = পৃথিবীর ভর, G = মহাকর্ষীয় ধ্রুবক, R = পৃথিবীর ব্যাসার্ধ এবং h = পাহাড়ের উচ্চতা
সমীকরণ (8.11)-কে সমীকরণ (8.12) দ্বারা ভাগ করে আমরা পাই,
সুতরাং R. g এবং g1-এর মান জেনে h এর মান নির্ণয় করা যায়।
সময় নির্ণয়
দোলক ঘড়িতে দোলকের সাহায্যে সময় মাপা হয়। এ সব দোলক সাধারণত ধাতুর দ্বারা নির্মিত। শীতকালে তারের দৈর্ঘ্য কমে যায় এবং গ্রীষ্মকালে দৈর্ঘ্য বেড়ে যায়। সুতরাং শীতকালে ঘড়ির দোলন কাল কমে যায় এবং ঘড়ি দ্রুত চলে। গ্রীষ্মকালে ঘড়ির দোলন কাল বেড়ে যায় এবং ঘড়ি ধীরে চলে। সাধারণ দোলক ঘড়ির পিণ্ডের নিচের একটি স্ক্রুকে প্রয়োজনমতো ঘুরিয়ে পিণ্ডকে উঠা-নামা করিয়ে দোলন কাল নিয়ন্ত্রণ করা হয়।
মাটির নিচে বা উঁচু পাহাড়ের উপর g-এর মান কম। কাজেই উঁচু পাহাড়ে বা মাটির নিচে দোলকের দোলন কাল বেশি হয়। এর অর্থ ঘড়ি ধীরে চলে। বিষুব অঞ্চলে g-এর মান কম এবং মেরু অঞ্চলে g-এর মান বেশি। অতএব একটি দোলক ঘড়িকে বিষুব অঞ্চল হতে মেরু অঞ্চলে নিলে ঘড়িটি দ্রুত চলে।










