শূন্যস্থানে আলোর বেগ সেকেন্ডে m/s, আলো যখন কোনো মাধ্যমে প্রবেশ করে তখন আলোর বেগ এর থেকে কমে যায় এবং এই প্রক্রিয়াটিকে ব্যাখ্যা করার জন্য প্রতিসরণাঙ্ক বলে একটি রাশি সংজ্ঞায়িত করা হয়েছে। তোমরা ইচ্ছে করলেই দেখাতে পারবে আলোর বেগের তারতম্যের জন্য এক মাধ্যম থেকে অন্য মাধ্যমে যাবার সময় আলোক রশ্মি বেঁকে যায়।
আলোর এই ধর্ম বা প্রতিসরণের কারণে পূর্ণ অভ্যন্তরীণ প্রতিফলন নামে একটি অত্যন্ত চমকপ্রদ ব্যাপার ঘটতে পারে। এই অধ্যায়ে আমরা পূর্ণ অভ্যন্তরীণ প্রতিফলনের নানা ধরনের ব্যবহার নিয়ে আলোচনা করব।
আলোর প্রতিসরণকে ব্যবহার করে উত্তল এবং অবতল লেন্স তৈরি করা যায়। এই দুই ধরনের লেন্স দিয়ে কোন ধরনের প্রতিবিম্ব তৈরি করা হয় সেগুলোও এই অধ্যায়ে আলোচনা করা
তোমরা এর মাঝে জেনে গেছ যে আলো যখন একটা মাধ্যম থেকে অন্য মাধ্যমে প্রবেশ করতে চায় তখন তিনটি ভিন্ন ভিন্ন ঘটনা ঘটে। একটা হচ্ছে প্রতিফলন যখন প্রথম মাধ্যম থেকে দ্বিতীয় মাধ্যমে যাবার সময় খানিকটা আলো আবার প্রথম মাধ্যমে ফিরে আসে এবং সে বিষয়টি আমরা আগের অধ্যায়ে আলোচনা করেছি। একটি হচ্ছে প্রতিসরণ যখন প্রথম মাধ্যম থেকে আলো দ্বিতীয় মাধ্যমে প্রবেশ করে যে বিষয়টি আমরা এই অধ্যায়ে আলোচনা করব। আরেকটি হচ্ছে শোষণ যখন খানিকটা আলো শোষিত হয় যে বিষয়টি আমরা আলোচনা করব না।
আলোর প্রতিসরণ বোঝার জন্য প্রতিসরণাঙ্ক বলে একটা রাশি () ব্যবহার করা হয়। আমরা জানি, শূন্য স্থানে আলোর বেগ m/s, এবং এটি যখন কোনো মাধ্যমের ভেতর দিয়ে যায় তখন এই বেগটি কমে যায়। একটি মাধ্যমে আলোর বেগ কত গুণ কমে যায় সেটাই হচ্ছে এই মাধ্যমটার প্রতিসরণাঙ্ক। যেমন পানিতে আলোর বেগ হচ্ছে m/s কাজেই পানির প্রতিসরণাঙ্ক হচ্ছে:
অর্থাৎ শূন্য স্থানে আলোর বেগ পানিতে আলোর বেগ থেকে 1.33 গুণ বেশি।
ফাইবার অপটিক ক্যাবলের কাচের তন্তুর প্রতিসরণাঙ্ক 1.5, কাজেই ফাইবারের ভেতর দিয়ে আলোর বেগ
| শূন্য মাধ্যম | 1.00 |
| ৰাতাস | 1.00029 |
| পানি | 1.33 |
| সাধারণ কাচ | 1.52 |
| হীরা | 2.42 |
ফাইবার অপটিক ক্যাবলের কাচের তন্তুর প্রতিসরণাঙ্ক 1.5, কাজেই ফাইবারের ভেতর দিয়ে আলোর বেগ
প্রতিসরণাঙ্ক একটি সংখ্যা এবং এর কোনো একক নেই। যেহেতু আলোর সর্বোচ্চ বেগ, কাজেই এর মান সবসময়ই 1 থেকে বেশি। 9.01 টেবিলে কিছু পদার্থের প্রতিসরণাঙ্ক দেওয়া হয়েছে। শূন্য মাধ্যমে স্বাভাবিকভাবেই এর মান হবে 1, বাতাসের প্রতিসরণাঙ্ক 1.00029, এটি 1 এর এত কাছাকাছি যে আমরা এটাকে 1 ধরেই হিসাব করব।
এখানে উল্লেখ্য, কোনো মাধ্যমের প্রতিসরণাঙ্ক বলতে হলে সেটি কোন তরঙ্গ দৈর্ঘ্যের আলোতে মাপা হয়েছে সেটি বলে দিতে হয়। কারণ আলোর প্রতিসরণাঙ্ক আলোর তরঙ্গ দৈর্ঘ্যের ওপর নির্ভর করে।
প্রতিসরণের সূত্র বোঝার জন্য যে বিষয়গুলো জানা প্রয়োজন ছিল সেগুলো জানা হয়েছে। প্রতিফলনের বেলায় আমরা আলোক রশ্মি যে বিন্দুতে পড়েছে সেই বিন্দু থেকে একটি লম্ব কল্পনা করে নিয়েছিলাম, এখানেও সেই একই বিষয়টি করতে হবে। 9.01 চিত্রটিতে লম্বের সাথে আপতিত রশ্মিটির কোণকে বলব আপতন কোণ, দ্বিতীয় মাধ্যমে লম্বের সাথে প্রতিসরিত রশ্মির কোণকে বলৰ প্রতিসরণ কোণ।
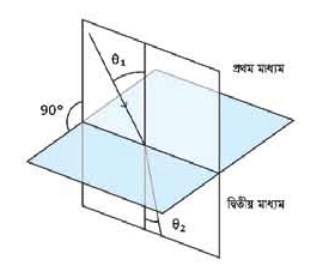
চিত্র 9.01: প্রথম মাধ্যম থেকে দ্বিতীয় মাধ্যমে আলোর প্রতিসরণ।
প্রতিসরণের প্রথম সুত্র: আপতন রশ্মি এবং লম্ব দিয়ে আমরা যে সমতলটি কল্পনা করে নিয়েছি প্রতিসরিত রশ্মি সেই একই সমতলে থাকবে।
প্রতিসরণের দ্বিতীয় সূত্র: প্রথম মাধ্যমের প্রতিসরণাঙ্ক দ্বিতীয় মাধ্যমের প্রতিসরণাঙ্ক , আপাতন কোণ , এবং প্রতিসরিত কোণ হলে
এই অতি সহজ সূত্রটি মনে রাখলে তুমি প্রতিসরণ-সংক্রান্ত সব সমস্যার সমাধান করে ফেলতে পারবে।
যদি প্রথম মাধ্যমটি বাতাস হয় তাহলে = 1 ধরে লিখতে পারি
যেহেতু এর মান 1 থেকে বেশি তাই অর্থাৎ প্রতিসরণের পর আলোক রশ্মিটি লম্বের দিকে বেঁকে যাবে। বেশি হলে আমরা অনেক সময় তাকে ঘন মাধ্যম বলি। মনে রাখতে হবে এখানে মাধ্যমের ভরের কারণে ঘন বলছি না। এটাকে ঘন বলতে বোঝানো হচ্ছে এর বেশি। কাজেই প্রতিসরণের দ্বিতীয় সূত্র থেকে আমরা বলতে পারি আলো হালকা মাধ্যম থেকে ঘন মাধ্যমে যাবার সময় প্রতিসরিত রশ্মি লম্বের দিকে বেঁকে যাবে। আবার ঘন মাধ্যম থেকে হালকা মাধ্যমে যাবার সময় সেটি লম্ব থেকে দূরে সরে যাবে।(চিত্র 9.02)
প্রতিসরণ নিয়ে আলোচনা করা হচ্ছে বলে এখানে শুধু আপতন রশ্মি এবং প্রতিসরিত রশ্মি আঁকা হয়েছে কিন্তু সবাইকে মনে রাখতে হবে যখনই একটি আলোক রশ্মি এক মাধ্যম থেকে অন্য মাধ্যমে প্রবেশ করে তখন সব সময়ই খানিকটা আলো প্রতিফলিত হয়। দুটো মাধ্যমের মাঝে কতখানি প্রতিফলিত হবে এবং কতখানি প্রতিসরিত হবে সেটা নির্ভর করে আপতন কোণের ওপর। আপতন কোণ বাড়তে থাকলে সব সময়ই প্রতিফলন বাড়তে থাকে।
আমরা বলেছি কোনো মাধ্যমের প্রতিসরণাঙ্ক সব সময় 1 থেকে বেশি হয়। কারণ প্রতিসরণাঙ্ক যেহেতু শূন্য মাধ্যমের সাথে সেই মাধ্যমে আলোর বেগের তুলনা এটা 1 থেকে বেশি হবে। মাঝে মাঝে এক মাধ্যমের প্রতিসরণাঙ্কের তুলনায় অন্য মাধ্যমের প্রতিসরণাঙ্ক প্রকাশ করা হয় তখন কোনটির সাথে কোনটির তুলনা করা হয়েছে তার ওপর নির্ভর করে সেটা 1 থেকে কম হতে পারে।
যেমন পানিকে প্রথম মাধ্যম এবং কাচকে দ্বিতীয় মাধ্যম ধরলে
পানির তুলনায় কাচের প্রতিসরণাঙ্ক
যেটি 1 থেকে বেশি।
আবার কাচের তুলনায় পানির প্রতিসরণাঙ্ক
যেটি 1 থেকে কম।
অর্থাৎ যে মাধ্যমের প্রতিসরণাঙ্ক বের করতে চাচ্ছ সেটিকে যার তুলনায় বের করতে চাইছ সেই প্রতিসরণাঙ্ক দিয়ে ভাগ দিতে হবে।
পানির তুলনায় হাঁরা: 1.82
হীরার তুলনায় পানি: 0.55
কাচের তুলনায় হীরা: 1.59
হীরার তুলনায় কাচ: 0.63
তবে পদার্থবিজ্ঞানে সাধারণত দুটির তুলনা হিসেবে প্রতিসরণাঙ্ক ব্যবহার না করে নির্দিষ্ট বস্তুর প্রতিসরণাঙ্ক হিসেবেই ব্যবহার করা হয়।
প্রতিফলন সম্পর্কে আলোচনা করার সময় বলা হয়েছিল যখন অত্যন্ত নিখুঁত এবং পূর্ণাঙ্গ প্রতিফলন প্রয়োজন হয় তখন আরনা ব্যবহার না করে পুরোপরি স্বচ্ছ মাধ্যম ব্যবহার করে এক ধরনের প্রতিফলন করানো হয়। এই প্রতিফলনের নাম পূর্ণ অভ্যন্তরীণ প্রতিফলন। এটি অত্যন্ত সহজ এবং চমকপ্রদ একটি প্রক্রিয়া, এখানে প্রতিসরণের নিয়ম ব্যবহার করে আলোক রশ্মিটি ঘন মাধ্যম থেকে হালকা মাধ্যমে পাঠাতে হয় মাত্র।
আমরা এর মাঝে জেনে গেছি (এবং অনেকবার ব্যবহার করেছি), প্রতিসরণের সূত্র হচ্ছে
অর্থাৎ যদি থেকে বড় হয় তাহলে থেকে ,বড় হবে। ধরা যাক তুমি একটি ঘন মাধ্যম () থেকে একটি আলোক রশ্মি হালকা মাধ্যমের () দিকে পাঠাচ্ছ । প্রতিসরণ এবং প্রতিফলনের নিয়ম অনুযায়ী খানিকটা আলো প্রতিফলিত হবে এবং খানিকটা প্রতিসরিত হবে।যেহেতু, থেকে বড় হবে কাজেই ° থাকতেই হয়ে যাবে এবং এর পর থেকে আলোর প্রতিসরিত হবার আর কোনো সুযোগ থাকবে না। অর্থাৎ যখন হবে তখন থেকে পুরো আলোকেই প্রতিফলিত হতে হবে। এর যে মানের জন্য হয় সেই কোণকে ক্লান্তি কোণ বা সংকট কোণ (Critical Angle) ও বলে।
অর্থাৎ
কিংবা
এবং এর মান জানা থাকলে আমরা একটি কোণ , বের করতে পারব যার জন্য উপরের সূত্রটি সত্যি। কাজেই সূত্রটাকে এভাবেও লেখা যেতে পারে:
কাচের = 1.52
বাতাসের = 1.00 হলে
এটা দেখানো সম্ভব যে
কাজেই ক্রান্তি কোণ
অর্থাৎ যদি স্বচ্ছ কাচ থেকে বাতাসের মাঝে আলো পাঠানের সময় আলোক রশ্মি 41.8° থেকে বেশি আপাতন কোণ করে তাহলে আলোক রশ্মিটি স্বচ্ছ কাচ থেকে বের না হয়ে পুরোপুরি প্রতিফলিত হয়ে যায়। তোমরা যদি একটি প্রিজম সংগ্রহ করতে পারো তাহলে খুব সহজেই পূর্ণ অভ্যন্তরীণ প্রতিফলন ব্যাপারটি নিজের চোখে দেখতে পাবে।
তোমরা যারা ভাবছ যে তোমরা সত্যি সত্যি কখনো পূর্ণ অভ্যন্তরীণ প্রতিফলন দেখনি তাদেরকে মনে করিয়ে দেওয়া যায় যে যারা রংধনু দেখেছে তারাই পূর্ণ অভ্যন্তরীণ প্রতিফলন দেখেছে। রংধনু তৈরি হয় পানির পূর্ণ অভ্যন্তরীণ প্রতিফলন দিয়ে।
শুধু তাই নয়, যারা প্রিজমের অভাবে সাদা আলোকে তার রংগুলোতে ভাগ করে দেখতে পারোনি তারাও এই ব্যাপারটি রংধনুতে ঘটতে দেখেছ। বৃষ্টি হবার পরপর যদি রোদ ওঠে তাহলে আমরা রংধনু দেখি। তার কারণ তখন বাতাসে পানির কণা থাকে এবং পানির কণায় সেই আলো পূর্ণ অভ্যন্তরীণ প্রতিফলিত হবার সময় ভিন্ন ভিন্ন রঙের আলো ভিন্ন ভিন্ন পরিমাণে বেঁকে যায়। এই আলোর রশ্মিগুলো দিয়ে রংধনুর ভিন্ন ভিন্ন রঙের ব্যান্ড (band) তৈরি হয়।
তোমরা যারা রংধনু দেখেছ তারা নিশ্চয়ই আবিষ্কার করেছ এটি সব সময়ই সূর্যের বিপরীত আকাশে দেখা যায় এবং এখন তার কারণটি নিশ্চয়ই বুঝতে পারছ।
মরুভূমিতে মরীচিকা খুবই পরিচিত দৃশ্য। তোমরা হয়তো শুনে অবাক হবে যে মরীচিকাও রংধনুর মতো পূর্ণ অভ্যন্তরীণ প্রতিফলনের কারণে ঘটে থাকে।
কোনো কিছু পাওয়ার আশা করে শেষ পর্যন্ত না পেলে সেটাকেও মরীচিকা বলা হয় কিন্তু মূল শব্দটি এসেছে মরুভূমিতে উত্তাপের কারণে বাতাসের ঘনত্বের পরিবর্তন থেকে। যদিও আমরা জানি উত্তপ্ত বাতাস হালকা বলে উপরে চলে যায় কিন্তু মরুভূমির উত্তপ্ত বালুর কারণে তার কাছাকাছি বাতাস উপরের বাতাস থেকে উত্তপ্ত থাকতে পারে। কাজেই মরুভূমির বাতাসকে আমরা 9.09 চিত্রের মতো করে কল্পনা করে নিতে পারি।

চিত্র 9,09:মরুভুমিতে বাতাসের ঘনত্বের পার্থক্যের কারণে মরীচিকা দেখা যায়
সহজভাবে বোঝানোর জন্য এখানে মাত্র কয়েকটি স্তরে দেখানো হয়েছে। উপরের স্তরে বাতাসের ঘনত্ব বেশি তাই প্রতিসরণাঙ্ক বেশি। নিচের স্তরে বাতাস উত্তপ্ত তাই ঘনত্ব কম এবং প্রতিসরণাঙ্কও কম। গাছ থেকে আলো প্রতিটি স্তরে প্রতিসরিত হবার সময় প্রতিসরণ কোণ বেড়ে যাবে এবং একেবারে নিচের স্তরে এসে পূর্ণ অভ্যন্তরীণ প্রতিফলন হয়ে যেতে পারে। বেশি প্রতিসরণাঙ্কের থেকে কম প্রতিসরণাঙ্কের মাধ্যমে যাবার সময় দূর থেকে দেখা হলে আপাতন কোণের মান বেশি হওয়ার কারণে ক্রান্তি কোণকে অতিক্রম করার সম্ভাবনা বেশি থাকে। তাই মরীচিকাকে দূর থেকে দেখা যায়, কাছে এলে দেখা যায় না। যেহেতু কোনো মানুষ দূরের একটি গাছের দিকে তাকালে সরাসরি গাছটি দেখতে পাবে এবং পূর্ণ অভ্যন্তরীণ প্রতিফলনের কারণে পাছের একটি প্রতিবিম্ব গাছের নিচেও দেখতে পাবে। মনে হবে নিচে পানি থাকার কারণে সেখানে গাছের প্রতিবিম্ব দেখা যাচ্ছে। কাছে গেলে দেখা যাবে কোনো পানি নেই।পরমের দিনে উত্তপ্ত রাস্তার গাড়ি চালিয়ে যাবার সময় একই কারণে দূরে কালচে ভেজা রাস্তা দেখা যায়। সেখানে পৌঁছানোর পর দেখা যার রাস্তাটি খটখটে শুকনো। এটাও এক ধরনের মরীচিকা।
আলোর প্রতিসরণের নানা ধরনের ব্যবহার রয়েছে। আমাদের জীবনের নানা ক্ষেত্রে যে ব্যবহারগুলো গুরুত্বপূর্ণ ভূমিকা পালন করে থাকে তোমাদের সেরকম কয়েকটি উদাহরণ দেওয়া যেতে পারে:
নতুন পৃথিবীর যোগাযোগের মাধ্যমে বৈদ্যুতিক তারকে অত্যন্ত সরু কাচের তন্তু দিয়ে পাল্টে দেওয়া হয়েছে। আগে যেখানে বৈদ্যুতিক সিগন্যাল দিয়ে তথ্য পাঠানো হতো এখন সেখানে আলোর সিগন্যাল দিয়ে তথ্য পাঠানো হয়। মুক্ত অবস্থায় আলো সরলরেখার যায় কিন্তু ফাইবারে আলো আটকা পড়ে যায় বলে সেটাকে ঘুরিয়ে পেঁচিয়ে যেকোনো দিকে নেওয়া সম্ভব।
অপটিক্যাল ফাইবার অত্যন্ত সরু কাচের তন্তু, এর ভেতরের অংশকে বলে কোর (core), বাইরের অংশকে বলে ক্ল্যাড (clad)। দুটিই একই কাচ দিয়ে তৈরি হলেও ভেতরের অংশের (কোর) প্রতিসরণাঙ্ক বাইরের অংশ থেকে বেশি। এ কারণে আলোকে পূর্ণ অভ্যন্তরীণ প্রতিফলনের মাধ্যমে কোরের মাঝে আটকে রেখে অনেক দূরে নিয়ে যাওয়া যায়। (চিত্র 9.10) অপটিক্যাল ফাইবার দিয়ে আলো শত শত কিলোমিটার নিয়ে যাওয়া যায়, কারণ এই কাচের তন্তুতে আলোর শোষণ হয় খুবই কম। দৃশ্যমান আলো হলে শোষণ বেশি হতো বলে ফাইবারে লম্বা তরঙ্গ দৈর্ঘ্যের ইনফ্রারেড বা অবলাল রশ্মি ব্যবহার করা হয়।
শেষ অধ্যায়ে এডোস্কোপি নামের চিকিৎসাবিজ্ঞানের একটি প্রক্রিয়ায় কীভাবে অপটিক্যাল ফাইবার ব্যবহার করা হয় সেটি বর্ণনা করা হয়েছে।
আমরা সবাই জানি সাবমেরিনে পেরিস্কোপ থাকে এবং সেই পেরিস্কোপ দিয়ে পানির নিচ থেকে পানির উপরের দৃশ্য দেখা সম্ভব। সাধারণ আয়না দিয়ে যে ধরনের পেরিস্কোপ তৈরি করা যায় তার থেকে অনেক বেশি কার্যকর পেরিস্কোপ তৈরি করা হয় প্রিজম এবং তার পূর্ণ অভ্যন্তরীণ প্রতিফলন দিয়ে। বাইনোকুলারের দৈর্ঘ্য কমানোর জন্যও এর ভেতরে প্রিজম দিয়ে পূর্ণ অভ্যন্তরীণ প্রতিফলন করা হয়ে থাকে।
কোনো স্বচ্ছ মাধ্যমের দুই পৃষ্ঠ সমান্তরাল না হলে তাকে গ্রিজম বলে। স্বচ্ছ সমান্তরাল মাধ্যমে বেদিকে আলো প্রবেশ করে সেই দিকের সাথে সমান্তরাল হয়ে আলোক রশ্মি বের হয়ে যায়। দিক অপরিবর্তিত থাকলেও আলোক রশ্মি মূল রশ্মি থেকে খানিকটা সরে যায়। প্রিজমের বেলায় আলোক রশ্মির দিক পাল্টে যায়। প্রথম পৃষ্ঠ দিয়ে আলোক রশ্মিটি প্রবেশ করার সময় লম্বের দিকে বেঁকে যায়। যেহেতু দ্বিতীয় পৃষ্ঠটি সমান্তরাল নয় তাই সেই পৃষ্ঠ দিয়ে আলো বের হবার সময় লম্ব থেকে সরে গেলেও সেটি আর মূল দিকে ঘুরে যেতে পারে না।
প্রিজমে আলোর দিক পাল্টে যাবার ঘটনা ঘটলেও সেটি অন্য একটি কারণে আরো বেশি পুরুত্বপূর্ণ। প্রিজমে একটি আলোক রশ্মি প্রবেশ করার পর সেটি মূল দিক থেকে কতটুকু বেঁকে যাবে সেটি প্রিজমের প্রতিসরণাঙ্কের ওপর নির্ভর করে। আমরা আগেই বলেছি প্রতিসরণাঙ্ক আসলে আলোর তরঙ্গ দৈর্ঘ্য বা রঙের ওপর নির্ভর করে। তাই ভিন্ন ভিন্ন রঙের জন্য প্রতিসরণাঙ্ক ভিন্ন, কাজেই একই আলোক রশ্মিতে ভিন্ন ভিন্ন রং থাকলে প্রিজমের ভেতর দিয়ে যাবার সময় সেই রঙের আলোগুলো ভিন্ন ভিন্ন কোণে দিক পরিবর্তন করবে। কাজেই আমরা দেখব প্রিজম থেকে আলো বের হবার সময় তার রংগুলো আলাদা হয়ে গেছে, নিউটন যেটি প্রথম দেখিয়েছিলেন।
আলোর প্রতিসরণ ব্যবহার করে লেন্স তৈরি করা হয়। এই লেন্স দিয়ে চশমা থেকে শুরু করে টেলিস্কোপ বা মাইক্রোস্কোপের মতো সূক্ষ্ম অপটিক্যাল যন্ত্রপাতি তৈরি করা হয়। ভিডিও প্রজেক্টর বা ক্যামেরাতেও লেন্স ব্যবহার করা হয়। এই অধ্যায়ে আমরা বিস্তৃতভাবে লেন্স, লেন্সের প্রকারভেদ এবং তার ধর্ম নিয়ে আলোচনা করব।
আমরা উত্তল এবং অবতল আয়না পড়ার সময় দেখেছি এই আয়নাগুলোর ভেতর দিয়ে আলো যাবার সময় কখনো একবিন্দুতে কেন্দ্রীভূত (অভিসারী রশ্মি) হয় আবার কখনো ছড়িয়ে পড়ে (অপসারী রশ্মি) এবং সে কারণে প্রতিবিম্বের তৈরি হয়। সেই প্রতিবিম্ব কখনো সত্যিকারের প্রতিবিম্ব হয় কখনো অবাস্তব হয়। কখনো ছোট হয় কখনো বড় হয়। আলোর এই প্রতিবিম্বকে নানাভাবে ব্যবহার করে বিভিন্ন ধরনের অপটিক্যাল যন্ত্রপাতি তৈরি করা হয়ে থাকে।
উত্তল এবং অবতল আয়না দিয়ে যে রকম নানা ধরনের প্রতিবিম্ব তৈরি করা হয় ঠিক সে রকম লেন্স দিয়েও নানা ধরনের প্রতিবিম্ব তৈরি হয় এবং নানাভাবে সেগুলো ব্যবহার হয়। আমরা সবাই লেন্স দেখেছি (তার কারণ চশমার কাচগুলো আসলে এক ধরনের লেন্স)। তোমাদের মাঝে যারা চশমা ব্যবহার করো কিংবা যারা অন্যদের চশমা ব্যবহার করতে দেখেছ তারা নিশ্চিতভাবেই লক্ষ করেছ যে চশমার লেন্সকে দুই ভাগে ভাগ করা যায়। এক ধরনের পেল দিয়ে ছোট জিনিসকে বড় দেখা যায়। (সাধারণত বয়স্কদের চশমার লেন্স এ রকম হয়।} আবার অন্য ধরনের লেন্স দিয়ে বড় জিনিসকে ছোট দেখা যায় (সাধারণত কম বয়সীদের চশমার লেন্স এ রকম হয়)। যে লেন্স দিয়ে ছোট জিনিসকে বড় দেখা যায় সেগুলোকে উত্তল (convex) কিংবা (কদাচিৎ) অভিসারী লেন্স বলে। যে লেন্স দিয়ে বড় জিনিসকে ছোট দেখা যায় সেই লেন্সগুলোকে অবতল লেন্স (concave) কিংবা কদাচিৎ) অপসারী লেন্স বলে। যে লেন্স দিয়ে ছোট জিনিসকে বড় দেখা যায় অর্থাৎ উত্তল লেন্সগুলোর মাঝখানের অংশ প্রান্ত থেকে পূর্ব্ব হয়। আর অবতল লেলগুলোর মাঝখানের অংশ প্রান্ত থেকে সরূ হয় 9.14 চিত্রটিতে যে রকম দেখানো হয়েছে। লেন্সের প্রস্থচ্ছেদের দিকে তাকালেই আমরা বুঝতে পারি উত্তল কিংবা অবতল লেন্সের দুটিই দুটি গোলীয় বৃত্ত দিয়ে সীমাবদ্ধ। এই দুটি গোলীয় বৃত্তের ব্যাসার্ধ সমানও হতে পারে ভিন্নও হতে পারে। এই বৃত্তগুলোর কেন্দ্রকে বক্রতার কেন্দ্র বলে।
দৈনন্দিন জীবনে বা বিজ্ঞানের নানা বিষয়ে নানা ধরনের লেন্স ব্যবহার করা হয়। তবে আমরা আমাদের এই বইয়ে আমাদের আলোচনা পাতলা লেন্সের মাঝে সীমাবদ্ধ রাখব। পাতলা লেন্স এবং পুরু লেন্সের পার্থক্য নামকরণ থেকেই বোঝা গেলেও আমরা পার্থক্যটুকু আরেকটু পরিষ্কার করে নিই। লেন্সের প্রস্থচ্ছেদের দিকে তাকালে আমরা দেখতে পাই যদিও লেন্সের পৃষ্ঠদেশের এক ধরনের বক্রতা আছে কিন্তু ঠিক মাঝামাঝি জায়গায় দুটি পৃষ্ঠ প্রায় সমান্তরাল। আমরা জানি সমান্তরাল পৃষ্ঠ দিয়ে আলো যাবার সময় প্রতিসরণের কারণে আলোক রশ্মিটি মূল দি থেকে খানিকটা বিচ্যুৎ হয়ে যায়। চিত্র 9.16)
সমান্তরাল পৃষ্ঠ দুটি যত পুরু হবে আলোক রশ্মিটি মূল রশ্মির দিক থেকে তত বেশি সরে যাবে। যদি সমান্তরাল পৃষ্ঠ দুটি খুব কাছাকাছি বিচ্যুত হয়। হয় তাহলে আমরা ধরে নিতে পারি মূল আলোক রশ্মি যে দিক দিয়ে এসেছে মোটামুটি সেদিক দিয়েই বের হয়েছে, তার কোনো বিস্তৃতি হয়নি। যেসব লেন্সের বেলায় তার কেন্দ্র দিয়ে আলোক রশ্মি যাবার সময় ধরে নেওয়া যায় যে রশ্মিটির দিক অপরিবর্তিত আছে সেই সব লেন্সকে পাতলা লেন্স বলে। কিংবা একটু অন্যভাবে বলতে পারি পাতলা লেন্সের মাঝখানের যে বিন্দু দিয়ে আলোক রশ্মি যাবার সময় বেঁকে যায় না সেটি হচ্ছে লেন্সের কেন্দ্র বা লেন্সের আলোকীয় কেন্দ্র (Optical Center)।
উত্তল এবং অবতল আয়না আলোচনা করার সময় আমরা প্রথমে উত্তল আয়না নিয়ে আলোচনা করেছিলাম। লেন্সের বেলায় আমরা প্রথমে অবতল লেন্স নিয়ে আলোচনা করি। কারণ উত্তল আয়নায় যে ধরনের প্রতিবিম্ব তৈরি হয় অবতল লেন্সে সেই একই ধরনের প্রতিবিম্ব তৈরি হয়।
উত্তল আয়নার বেলায় আমরা দেখেছিলাম সেখানে সমান্তরাল আলো পড়লে সেটি প্রতিফলিত হবার সময় চারদিকে ছড়িয়ে পড়ে। অবতল লেন্সের বেলাতেও ঠিক এই ধরনের ব্যাপার ঘটে। এই লেন্সে সমান্তরাল আলো পড়লে প্রতিসরিত হবার সময় সেটি ছড়িয়ে পড়ে। প্রতিসরিত আলোগুলো যদি আমরা পেছনের দিকে বাড়িয়ে নিই তাহলে মনে হবে সেগুলো বুঝি একটি বিন্দু থেকে সোজা ছড়িয়ে পড়ছে। সেই বিন্দুটিকে বলে ফোকাস বিন্দু এবং লেন্সের কেন্দ্র থেকে এই ফোকাস পয়েন্টের দূরত্বটিকে বলে ফোকাস দূরত্ব।
উত্তল আয়নার বেলায় আমরা শুধু এক দিক থেকে আয়নার ওপর আলো ফেলতে পারতাম। লেন্সের বেলায় দুই দিক থেকেই আলো ফেলা যায়। প্রত্যেকটা লেন্সের একটা ফোকাস দূরত্ব থাকে। আলো যেদিক দিয়েই ফেলা হোক তার ফোকাস দূরত্ব সমান থাকে। সমান্তরাল আলো ফেলা হলে সেটি ছড়িয়ে পড়ে এবং মনে হয় সেটি বুঝি ফোকাস বিন্দু থেকে বিচ্ছুরিত হয়ে ছড়িয়ে পড়ছে। আলোক রশ্মির গতিপথ উল্টো করে দিলে এটি যেদিক দিয়ে এসেছে ঠিক সেদিক দিয়ে ফিরে যায়। তাই অবতল লেন্সের ছড়িয়ে যাওয়ার আলোর গতিপথ কোনোভাবে উল্টো করে দিতে পারলে সেটি সমান্তরাল হয়ে উল্টো দিকে বের হয়ে যাবে। (চিত্র 9.19)
অবতল লেন্সে কীভাবে প্রতিবিম্ব তৈরি হয় সেটি বোঝার জন্য আলোক রশ্মি অবতল লেন্সে কীভাবে প্রতিসরিত হয় সেটি জানতে হবে। সেটি নির্ভর করে আলোক রশ্মি কী কোণে অবতল লেন্সে এসে পড়ছে তার উপর। আমরা তিনটি বিশেষ আলোক রশ্মির প্রতিসরণের নিয়ম জানলেই কীভাবে প্রতিবিম্ব তৈরি হয় সেটি ব্যাখ্যা করতে পারব :
(i) আলোক রশ্মি কেন্দ্রমুখী হলে সেটি প্রতিসরণের পর সোজাসুজি চলে যায়।
(11) প্রধান অক্ষের সমান্তরাল রশ্মিটি প্রতিসরণের পর মনে হবে যেন রশ্মিটি ফোকাস বিন্দু থেকে আসছে।
(iii) আলোক রশ্মির দিক পরিবর্তন করা হলে এটি যেদিক থেকে এসেছে ঠিক সেদিক দিয়ে ফিরে যায়। কাজেই কোনো আলোক রশ্মি ফোকাস অভিমুখী হলে সেটি প্রধান অক্ষের সাথে সমান্তরাল হয়ে প্রতিসরিত হবে।
আমরা এখন ইচ্ছে করলে অবতল লেন্সে একটা বস্তুর প্রতিবিম্ব কেমন হবে সেটা বের করতে পারি। ধরা যাক একটা বস্তু XY একটা অবতল লেন্সের কাছে রাখা হয়েছে। (চিত্র 9.20) বিশ্লেষণটি সহজ করার জন্য ধরে নিয়েছি বস্তুটির Y বিন্দুটি লেন্সের মূল অক্ষ YR এর উপরে। বস্তুটির কোন বিন্দুর প্রতিবিম্বটি কোথায় হবে সেটি বের করার জন্য সেই বিন্দু থেকে অন্তত দুটি রশ্মি আঁকা দরকার।
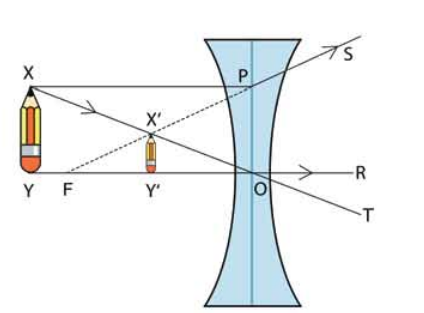
চিত্র 9.20: অবতল লেন্সে একটি বস্তুকে ছোট দেখায়।
Y বিন্দু থেকে দুটি রশ্মি না এঁকেও আমরা প্রতিবিম্বটি বের করতে পারব। Y বিন্দু থেকে YR অক্ষ বরাবর একটি রশ্মি আঁকা সম্ভব, তাই আমরা জানি Y বিন্দুটির প্রতিবিম্ব এই অক্ষের ওপর তৈরি হবে। X বিদুটির প্রতিবিম্ব থেকে অক্ষের ওপর লম্বটি এঁকে নিলেই আমরা Y বিন্দুর প্রতিবিম্ব পেরে যাব।
X বিন্দু থেকে দুটি রশ্মি কল্পনা করি, একটি অক্ষের সাথে সমান্তরাল XP সেটি লেন্স থেকে বের হওয়ার সময় ছড়িয়ে যাবে এবং যেহেতু মনে হবে ফোকাস থেকে বিচ্ছুরিত হচ্ছে তাই ফোকাস F থেকে P পর্যন্ত একটি রেখা টেনে বর্ধিত করলেই সেই রশ্মিটি পেয়ে যাব। দ্বিতীয় রশ্মিটি x বিন্দু থেকে লেন্সের কেন্দ্রের দিকে এঁকে নিই। পাতলা লেন্সের নিয়ম অনুযায়ী এটি সরাসরি XT দিকে বের হয়ে যাবে। XT এবং PS রেখা দুটি যে বিন্দুতে ছেদ করবে সেটিই হচ্ছে X এর প্রতিবিম্ব X, X' থেকে অক্ষের ওপর লম্ব আঁকলে আমরা XY এর প্রতিবিম্ব X'Y' পেয়ে যাব।
উত্তল আয়নার বেলায় আমরা যা দেখেছিলাম অবতল লেন্সের প্রতিবিম্বের বেলাতেও সেটি সত্যি
(a) এটার অবস্থান হবে লেন্সের কেন্দ্র এবং ফোকাস বিন্দুর মাঝখানে
(b) এটা অবাস্তব
(c) এটা সোজা এবং এটা
(d) ছোট।
উত্তল লেন্সের প্রতিবিষগুলো অনেক চমকপ্রদ। অবতল আয়নায় আমরা যে ধরনের প্রতিবিম্ব পেয়েছিলাম উত্তল লেন্সে ঠিক সেই একই ধরনের প্রতিবিম্ব পাওয়া যায়। অবতল আয়নায় আমরা দেখেছিলাম তার ওপর সমান্তরাল রশ্মি ফেলা হলে সেটি ফোকাস বিন্দুতে এসে কেন্দ্রীভূত হয়। উত্তল লেন্সেও ঠিক একই ব্যাপার ঘটে, সমান্তরাল রশ্মি ফেলা হলে সেগুলো এই লেন্সের ফোকাস বিন্দুতে কেন্দ্ৰীভূত হয় এবং তারপর আবার ছাড়িয়ে যায়।কাজেই আগের যুক্তি ব্যবহার করে বলা যায় যদি কোনো বিন্দু থেকে আলো বিচ্ছুরিত হয় এবং একটা উত্তল লেন্সের ফোকাস বিন্দুতে সেই বিচ্ছুরিত ভালো উৎসটাকে রাখা যার তাহলে আলোটা লেন্সের ভেতর দিয়ে যাবার সময় সমান্তরাল রশ্মি হয়ে যাবে। (আলোর বেলায় এটি সব সময় সত্যি, এটি যদি A থেকে B তে যায় তাহলে রশ্মির দিক পরিবর্তন করে দিলে এটি সব সময় B থেকে A তে যাবে।) এখন আমরা ভিন্ন ভিন্ন অবস্থানে একটা বস্তু থাকলে তার প্রতিবিম্ব কোথায় হবে সেটি বের করে ফেলি।
সেটি শুরু করার আগে আমরা আলোক রশ্মি উত্তল লেন্সে কীভাবে প্রতিসরিত হয় সেটি জেনে নিই। উত্তল লেন্সে তিনটি বিশেষ আলোক রশ্মির প্রতিসরণের নিয়ম জানলেই কীভাবে প্রতিবিম্ব তৈরি হয় সেটি ব্যাখ্যা করতে পারব :
(1) আলোক রশ্মি কেন্দ্ৰমূখী হলে সেটি প্রতিসরণের পর সোজাসুজি চলে যায়।
(ii) প্রধান অক্ষের সমান্তরাল রশ্মিটি প্রতিসরণের পর ফোকাস বিন্দু দিয়ে যাবে
(iii) আলোক রশ্মির দিক পরিবর্তন করা হলে এটি যেদিক থেকে এসেছে ঠিক সেদিক দিয়ে ফিরে যায়। কাজেই কোনো আলোক রশ্মি ফোকাস দিয়ে গেলে সেটি প্রধান অক্ষের সাথে সমাস্তরাল হয়ে প্রতিসরিত হবে।
এবারে আমরা উত্তল লেন্সের জন্য প্রতিবিম্ব তৈরি করতে পারব।
ফোকাস দূরত্ব থেকে কম দূরত্ব
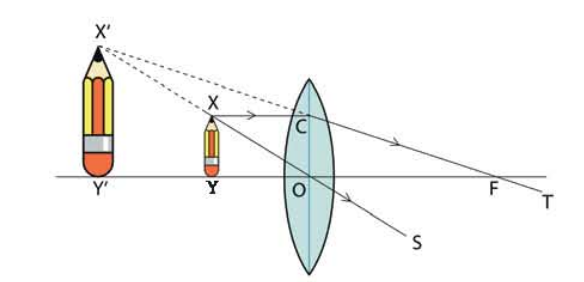
চিত্র 9.23: ফোকাস দূরত্বের ভেতরে বস্তু রাখা হলে উত্তল লেন্সে বড় প্রতিবিম্ব দেখা যায়।
প্রথমে ধরা যাক একটি বস্তু XY কে লেন্স এবং তার ফোকাস বিন্দুর F মাঝখানে রাখা হলো। (চিত্র 9.04) আগে যেভাবে ব্যাখ্যা করা হয়েছে ঠিক সেই একই যুক্তিতে বলতে পারি Y বিন্দুর প্রতিবিম্বটি YOF অক্ষ রেখার ওপর হবে। X বিন্দুটির প্রতিবিম্ব X' থেকে এই অক্ষের ওপর লম্ব আঁকা হলেই আমরা Y এর প্রতিবিম্বের অবস্থান পেরে যাব।
এবারে x বিন্দু থেকে দুটি রশ্মি আঁকি, অক্ষের সাথে সমান্তরাল XC রেখাটি ফোকাস বিন্দু F এর ভিতর দিয়ে T এর দিকে যাবে। x বিন্দু থেকে রশ্মি লেন্সের কেন্দ্রবিন্দু দিয়ে আঁকা হলে সেটি সোজা সরলরেখায় XO হয়ে $ এর দিকে যাবে। দেখতেই পাচ্ছ CFT এবং XOS রেখা দুটি সামনে গিয়ে মিলিত হতে পারবে না। যার অর্থ বাস্তব প্রতিবিম্ব তৈরি হবার কোনো সুযোগ নেই। রেখা দুটো পেছন দিকে বাড়িয়ে দিলে যে X' বিন্দুতে মিলিত হবে সেটাই X বিন্দুর প্রতিবিম্ব।
এই বিন্দু থেকে YF রেখার উপর লম্ব আঁকা হলে Y' বিন্দুতে স্পর্শ করে সেটা Y বিন্দুর প্রতিবিম্ব।
দেখাই যাচ্ছে XY বস্তুটি যতই লেন্সের কাছাকাছি আনা হবে প্রতিবিম্বটি ততই বড় হতে থাকবে। আবার বস্তুটি যতই ফোকাস বিন্দু F এর কাছাকাছি আনা হবে প্রতিবিম্বটি ততই বড় হতে থাকবে। বস্তুটি যখন ঠিক ফোকাস বিন্দু F এর ওপর হবে তখন প্রতিবিম্বটির আকার হবে অসীম। আমরা এখন বলতে পারি যদি একটা উত্তল লেন্সের কেন্দ্রবিন্দু এবং ফোকাস বিদুর মাঝখানে একটি বস্তু রাখা হয় তাহলে বস্তুটির প্রতিবিম্ব
(a) যে দিকে বস্তুটি রয়েছে সেই দিকেই তৈরি হবে
(b) প্রতিবিম্বটি হবে অবাস্তব
(c) সোজা এবং
(d) বড়।
ফোকাস দূরত্বের বাইরে
এবারে আমরা দেখি বস্তুটি ফোকাস দূরত্ব থেকে বাইরে রাখলে কী হয়। অবতল আয়নার মতো এখানেও তিনটি ভিন্ন ভিন্ন বিষয় হতে পারে। (1) বস্তুটি ফোকাস দূরত্বের বাইরে কিন্তু দ্বিগুণ ফোকাস দূরত্বের ভেতরে (ii) বস্তুটি দ্বিগুণ ফোকাস দূরত্বের বাইরে এবং (iii) বস্তুটি ঠিক দ্বিগুণ ফোকাস দূরত্বে। একটি একটি করে দেখা যাক।
(i) প্রথমে বস্তুটিকে ফোকাস দূরত্বের বাইরে কিন্তু ফোকাস দূরত্বের দ্বিপুণ দৈর্ঘ্যের ভেতরে রাখা হবে। 9.24 চিত্রটিতে XY বস্তুটির Y বিদুর প্রতিবিম্বটি YO রেখার উপরে হবে তাই আগের মতো আমরা শুধু X বিন্দুটির প্রতিবিম্ব বের করি। x বিন্দু থেকে অক্ষের সাথে সমান্তরাল রশ্মিটি ফোকাস বিন্দু F এর ভেতর দিয়ে যাবে। লেন্সের কেন্দ্রবিন্দু দিয়ে অন্য একটি রশ্মি XO সরলরেখায় যাবে। দুটি রেখা যেখানে ছেদ করবে সেই X বিন্দুটি হচ্ছে X এর প্রতিবিম্ব। X' থেকে অক্ষ YO রেখার ওপর লম্ব আঁকা হলে Y' বিন্দুটি হবে Y এর প্রতিবিম্বের অবস্থান। কাজেই XY' হচ্ছে XY এর প্রতিবিম্ব।
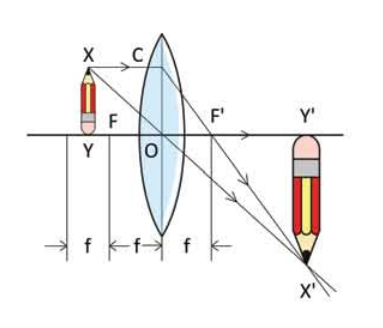
চিত্র 9.24: ফোকাস দূরত্বের বাইরে কিন্তু দ্বিগুণ ফোকাস দূরত্বের ভেতরে বস্তু রাখা হলে তার বাস্তব উল্টো বড় প্রতিবিম্ব তৈরি হয়।
অর্থাৎ এই প্রতিবিম্বের জন্য আমরা বলতে পারি :
(a) প্রতিবিম্বটির অবস্থান হবে ফোকাস দূরত্বের দ্বিপুণ দূরত্বের বাইরে
(b) বাস্তব (c) উল্টো
(d) এবং বস্তুর আকার থেকে বড়
(ii) এবারে আমরা দেখি বস্তুটি ফোকাস দূরত্বের ঠিক দ্বিগুণ দূরত্বে রাখা হলে কী হয়। দেখতেই পাচ্ছি XY বস্তুটি যদি ঠিক ফোকাস দূরত্বের দ্বিপুণ দুরত্বে (চিত্র 9.25) রাখা হয় তাহলে প্রতিবিম্বটির আকার হবে XY বস্তুটির সমান এবং প্রতিবিম্বটির অবস্থান হবে লেন্সের কেন্দ্র থেকে ঠিক সমান দূরত্বে। বস্তুটি যতই ফোকাস বিন্দুর কাছাকাছি আনা হতে থাকবে প্রতিবিম্বটি ততই দূরে তৈরি হবে এবং তার আকার বড় হতে থাকবে। যেহেতু এই প্রতিবিম্বের ভেতর দিয়ে সত্যিকার আলোক রশ্মি যায় ভাই এটি বাস্তব প্রতিবিম্ব এবং ছবিটিতে স্পষ্ট দেখা যাচ্ছে প্রতিবিম্বটি উল্টো 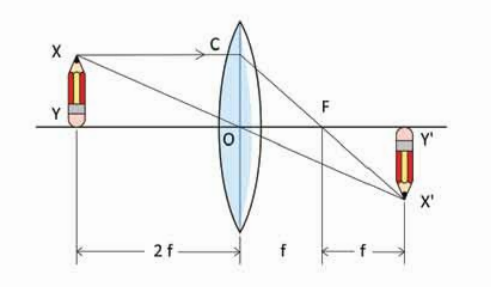
চিত্র 9.25: ঠিক ফোকাস দূরত্বের দ্বিগুণ দুরত্বে কোনো বস্তু রাখা হলে তার প্রতিবিম্বটি হবে বস্তুটির সমান
অর্থাৎ:
(a) প্রতিবিম্বটির অবস্থান হবে ফোকাস দূরত্বের দ্বিগুণ দূরত্বে
(b) বাস্তব
(c) উল্টো
(d) এবং বস্তুর সমান
(iii) এখন আমরা দেখি বস্তুটি যদি ফোকাস দূরত্বের ত্রিগুণ দুরত্বের বাইরে থাকে তাহলে তার কী ধরনের প্রতিবিম্ব কোথায় তৈরি হয়। এই প্রতিবিম্বটি আঁকার পদ্ধতি ঠিক আগেরটির মতো শুধু (চিত্র 9.26) বস্তুটিকে বসাতে হবে ফোকাস দূরত্বের দ্বিগুণ দূরত্বের বাইরে। আমরা আগেই বলেছি বস্তুটি যদি ফোকাস দূরত্বের দ্বিগুণ দূরত্বে রাখা হয় তাহলে তার সমদূরত্বে সমান আকারের একটা প্রতিবিম্ব তৈরি হয়। যতই বস্তুটা দূরে সরিয়ে নেওয়া হতে থাকে প্রতিবিম্বটি ততই ছোট হতে থাকে এবং ফোকাস বিন্দুর দিকে এগিয়ে আসতে থাকে। বস্তুটি যদি অসীম দূরত্বে সরিয়ে নেওয়া হয় তাহলে তার প্রতিবিম্বটি তৈরি হবে ঠিক ফোকাস বিন্দুতে।
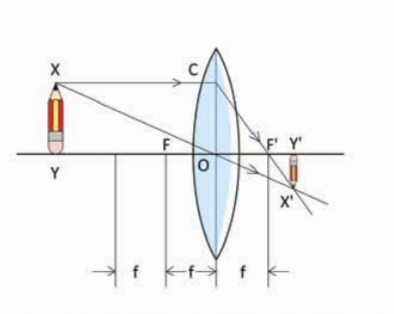
চিত্র 9.26:দ্বিগুণ ফোকাস দূরত্বের বাইরে বস্তু রাখা হলে তার ছোট উল্টো বাস্তব প্রতিবিম্ব তৈরি হয়
কাজেই ফোকাস দূরত্বের দ্বিগুণ দূরত্বের বাইরে কোনো বস্তু রাখা হলে বস্তুটির
(a) প্রতিবিম্বের অবস্থান হয় ফোকাস দূরত্ব এবং ফোকাস দূরত্বের দ্বিগুণ দূরত্বের মাঝখানে
(b) বাস্তব
(c) উল্টো
(d) ছোট।
লেন্সের সবচেয়ে প্রচলিত ব্যবহার আমরা দেখি চশমার মাঝে। তোমরা যদি বিভিন্ন মানুষের চশমার লেন্স পরীক্ষা করে দেখো তাহলে দেখবে কারো কারো চশমার লেন্স তৈরি হয় উত্তল লেন্স দিয়ে, কারো কারো চশমার লেন্স তৈরি হয় অবতল লেন্স দিয়ে। আমরা লেন্সগুলোকে প্রায় সময়ই পাওয়ার দিয়ে ব্যাখ্যা করি। তোমরা নিশ্চয়ই বলেছ কিংবা বলতে শুনেছ, অমুকের চশমার পাওয়ার অনেক বেশি। পাওয়ার কথাটি দিয়ে আমরা কী বোঝানোর চেষ্টা করি?
পাওয়ারের ধারণাটি এসেছে লেন্স দিয়ে বড় এবং ছোট দেখার ব্যাপারটি থেকে। দুটি উত্তল লেন্স দিয়ে যদি একটি জিনিসকে লেন্সের কাছাকাছি একই দূরত্বে রেখে দেখি এবং একটি লেন্সে জিনিসটি অন্য লেন্সটি থেকে বড় দেখায় তাহলে যে লেন্সটিতে বড় দেখায় আমরা বলি সেই লেলের পাওয়ার বেশি। তোমরা একটু চিন্তা করলেই দেখবে আসলে যে লেন্সের ফোকাস দূরত্ব যত কম সেই লেন্সে জিনিসটিকে তত বড় দেখাৰে।(চিত্র 9.27)
কাজেই লেন্সের পাওয়ার P হচ্ছে ফোকাস দূরত্বের ব্যস্তানুপাতিক। যদি ফোকাস দূরত্ব f মিটারে দেওয়া হয় তাহলে পাওয়ার P এর একক ডায়াপার। অর্থাৎ তোমার পরিচিত কারো চশমার পাওয়ার যদি হয় 2.5 (সাধারণ কথাবার্তায় ডায়াপটার শব্দটা কেউ ব্যবহার করে না।) তাহলে তার চশমার লেন্সের ফোকাস দূরত্ব হবে
(এককটি মিটারে)
পাওয়ারের ধারণাটি শুধু উত্তল লেন্সের বড় দেখানোর জন্য নয়। অবতল লেন্সে ছোট দেখানোর সময়ও একই পাওয়ার শব্দটি ব্যবহার করা হয়। যে অবতল লেন্সে কস্তুকে (সমান দূরত্বে) যত ছোট দেখা যাবে বুঝতে হবে তার পাওয়ার তত বেশি বা ফোকাস দূরত্ব তত ছোট। উত্তল লেলের বেলায় পাওয়ার ধনাত্মক বা পজিটিভ, অবতল লেন্সের বেলায় পাওয়ার ঋণাত্মক বা নেগেটিভ এটাই হচ্ছে পার্থক্য।
চোখের উপাদানগুলোর মাঝে রয়েছে রেটিনা, চোখের লেল, অ্যাকুয়াস হিউমার, ভিট্রিয়াস হিউমার এবং কর্নিয়া (চিত্র 9.28 )। তোমরা লেন্স কীভাবে কাজ করে তার একটি ধারণা পেয়েছ। তাই নিশ্চয়ই বুঝতে পারছ চোখের লেন্সও একটি উত্তল লেন্সের মতো কাজ করে। আমরা দেখেছি উত্তল বা অভিসারী লেন্স সব সময় উল্টো প্রতিবিম্ব তৈরি করে। ক্যামেরায় ছবি তোলার জন্য এভাবে প্রতিবিম্ব তৈরি করা হয়। যখনই আমাদের সামনে কোনো বস্তু থাকে, তখন ঐ বস্তুর থেকে আলোক রশ্মি এই লেন্স দ্বারা প্রতিসারিত হয় এবং রেটিনার ওপর একটি উল্টো প্রতিবিম্ব তৈরি করে। রেটিনার ওপর আলো পড়লে স্নায়ুর সাথে সংযুক্ত আলোকসংবেদী করে তাকে তড়িৎ বা বিদ্যুৎ সিগন্যালে পরিণত করে। স্নায়ু এই বিদ্যুৎ বা তড়িৎ সিগন্যালকে তাৎক্ষণিকভাবে অপটিক নার্ভ বা অক্ষি স্নায়ুর মাধ্যমে মস্তিক্ষে পাঠায়। মস্তিক রেটিনার সৃষ্ট উল্টো প্রতিবিম্বকে সোজা করে নেয় বলে আমরা বস্তুটির যে রকম থাকে সেরকমই দেখি। চোখের ভেতরে আলোর পরিমাণ বাড়ানো কিংবা কমানোর জন্য রয়েছে আইরিশ। তোমরা যারা আগে কখনো লক্ষ করোনি তারা চোখের ওপর টর্চলাইটের আলো ফেলে দেখতে পারো আইরিশটা কী চমৎকারভাবে সংকুচিত হয়ে পিউপিলটাকে ছোট করে ফেলে।
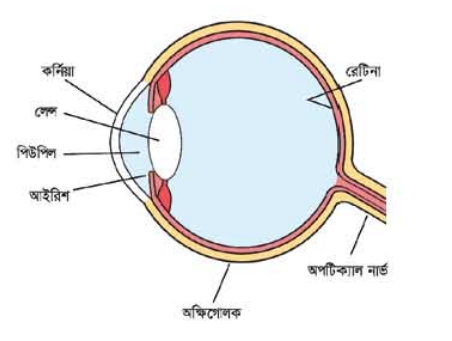
চিত্র 9.28 ঃ চোখের বিভিন্ন অংশ
কোনো কিছু ভালো করে দেখার জন্য আমরা সেটিকে আমাদের চোখের কাছে নিয়ে আসি। তোমরা নিশ্চয়ই লক্ষ করেছ চোখের বেশি কাছে নিয়ে আসা হলে আবার সেটি অস্পষ্ট হতে শুরু করে। মানুষের চোখের লেন্স অনেক চমকপ্রদ, এর সাথে মাংসপেশি লাগানো থাকে এবং এই মাংসপেশি লেন্সটাকে টেনে কিংবা ঠেলে পুরু কিংবা সরু করে ফোকাস দৈর্ঘ্য বাড়াতে কিংবা কমাতে পারে।কাজেই রেটিনার ওপর স্পষ্ট প্রতিবিম্ব তৈরি করার জন্য লেন্সটি সব সময়ই তার ফোকাস দৈর্ঘ্য বাড়িয়ে কিংবা কমিয়ে যাচ্ছে। তোমরা নিজেরা খুব সহজে এটা পরীক্ষা করতে পারো, চোখের সামনে একটি আঙ্গুল রেখে একই সাথে এই আঙ্গুলটি এবং দূরের কিছু দেখার চেষ্টা করো। যখন আঙ্গুলটি স্পষ্ট করে দেখবে তখন দূরের জিনিসটি ঝাঁপসা দেখাবে আবার দূরের জিনিসটি যখন স্পষ্ট দেখাবে তখন আঙ্গুলটি ঝাঁপসা দেখাবে। যেকোনো দুরত্বের কোনো লক্ষ্যবস্তু দেখার জন্য চোখের লেন্সের ফোকাস দূরত্ব নিয়ন্ত্রণ করার এই ক্ষমতাকে চোখের উপযোজন বলে।
লক্ষ্যবস্তু চোখের কাছাকাছি একটি নির্দিষ্ট দূরত্ব থেকে বেশি কাছে এলে আর স্পষ্ট দেখা যায় না । চোখের সবচেয়ে কাছে যে বিন্দু পর্যন্ত লক্ষ্যবস্তুকে খালি চোখে স্পষ্ট দেখা যায়, তাকে স্পষ্ট দৃষ্টির নিকট বিন্দু বলে এবং চোখ থেকে ঐ বিন্দুর দূরত্বকে স্পষ্ট দৃষ্টির ন্যূনতম দূরত্ব ধরে নেওয়া হয়। এই দূরত্ব মানুষের বয়সের সঙ্গে সঙ্গে পরিবর্তিত হয়। একজন শিশুর এই দূরত্ব 5 সেন্টিমিটারের কাছাকাছি এবং একজন স্বাভাবিক বয়স্ক লোকের এই দূরত্ব 25 সেন্টিমিটার পর্যন্ত হতে পারে।
সবচেয়ে বেশি যে দূরত্বে কোনো বস্তু থাকলে সেটি স্পষ্ট দেখা যায় সেটাকে চোখের দূরবিন্দু বলে। স্বাভাবিক চোখের জন্য দূরবিন্দু অসীম, যে কারণে আমরা কয়েক আলোকবর্ষ দূরের নক্ষত্রও স্পষ্ট দেখতে পাই ।
আমরা জানি সুস্থ এবং স্বাভাবিক চোখ “নিকট বিন্দু” (Near point) থেকে শুরু করে অসীম দূরত্বের দূরবিন্দুর মাঝখানে যে স্থানেই কোনো বস্তু থাকুক না কেন সেটা স্পষ্ট দেখতে পারে। এটাই চোখের স্বাভাবিক দৃষ্টিশক্তি। এই স্বাভাবিক দৃষ্টিশক্তি ব্যাহত হলেই তাকে চোখের দৃষ্টির ত্রুটি বলা হয়।
চোখের দৃষ্টির অনেক ধরনের ত্রুটি থাকলেও আমরা প্রধান দুটি ত্রুটি নিয়ে আলোচনা করব। সেই দুটি হচ্ছে;
(a) হ্রস্বদৃষ্টি বা ক্ষীণদৃষ্টি
(b) দীর্ঘদৃষ্টি বা দূরদৃষ্টি
যখন চোখ কাছের বস্তু দেখতে পায় কিন্তু দূরের বস্তু দেখতে পায় না, তখন চোখের এই ত্রুটিকে হ্রস্বদৃষ্টি বলে। এরূপ চোখের দূরবিন্দুটি অসীম দূরত্ব না হয়ে কাছে থাকে এবং বস্তুকে স্পষ্ট দৃষ্টির ন্যূনতম দূরত্ব থেকে আরও কাছে আনলে অধিকতর স্পষ্ট দেখায়। নিম্নলিখিত দুটি কারণে এই জুটি হয়ে থাকে।
(1) চোখের লেন্সের অভিসারী শক্তি বৃদ্ধি পেলে বা ফোকাস দূরত্ব কমে গেলে ও
(ii) কোনো কারণে অক্ষিগোলকের ব্যাসার্ধ বৃদ্ধি পেলে।
এর ফলে দূরের বস্তু থেকে আসা আলোক রশ্মি চোখের লেলের মধ্য দিয়ে প্রতিসরণের পর রেটিনার উপরে প্রতিবিম্ব তৈরি না করে একটু সামনে প্রতিবিম্ব তৈরি করে । ফলে চোখ বস্তুটি স্পষ্ট দেখতে পায় না।
প্রতিকার
এই জুটি দূর করার জন্য এমন একটি অবতল লেন্সের চশমা ব্যবহার করতে হবে। চশমার এই লেন্সের অপসারী ক্রিয়া চোখের উত্তল লেন্সের অভিসারী ক্রিয়ার বিপরীত, কাজেই চোখের ফোকাস দূরত্ব বেড়ে যাবে বলে প্রতিবিম্বটি আরো পেছনে তৈরি হবে। অর্থাৎ অসীম দূরত্বের বস্তু থেকে আসা সমান্তরাল আলোক রশ্মি চশমার অবতল লেন্স এর মধ্য দিয়ে চোখে পড়ার সময় প্রয়োজনমতো অপসারিত হয়। এই অপসারিত রশ্মিগুলো চোখের লেন্সে প্রতিসরিত হয়ে ঠিক রেটিনা বা অক্ষিপটে এর স্পষ্ট প্রতিবিম্ব তৈরি করে।
যখন কোনো চোখ দূরের বস্তু দেখে কিন্তু কাছের বস্তু দেখতে পায় না তখন এই ত্রুটিকে দীর্ঘদৃষ্টি বলে। সাধারণত বয়স্ক ব্যক্তিদের মধ্যে এই ত্রুটি দেখা যায়। নিম্নলিখিত দুটি কারণে এই ত্রুটি ঘটে।
(i) চোখের লেন্সের অভিসারী ক্ষমতা হ্রাস পেলে বা চোখের লেন্সের ফোকাস দূরত্ব বেড়ে গেলে।
(ii) কোনো কারণে অক্ষিগোলকের ব্যাসার্ধ কমে গেলে।
এর ফলে দূর থেকে আসা আলো সঠিকভাবে চোখের রেটিনাতে প্রতিবিম্ব তৈরি করলেও কাছাকাছি বিন্দু থেকে আসা আলোক রশ্মি চোখের লেন্সের মধ্য দিয়ে প্রতিসরণের পর রেটিনার ঠিক উপরে না হয়ে পেছনে বিন্দুতে মিলিত হয়। ফলে চোখ কাছের বস্তু স্পষ্ট দেখতে পায় না।
প্রতিকার
এই ত্রুটি দূর করার জন্য একটি উত্তল লেন্সের চশমা ব্যবহার করতে হবে। ফলে কাছাকাছি বিন্দু(চিত্র9.29 b) থেকে আসা আলোক রশ্মি চশমার লেন্সে এবং চোখের লেন্সে পর পর দুইবার প্রতিসারিত হওয়ার কারণে ফোকাস দূরত্ব কমে যাবে এবং প্রয়োজনমতো অভিসারী হয়ে প্রতিবিম্বটি রেটিনা(R) এর উপরে পড়বে।
চোখ অত্যন্ত চমকপ্রদ বিষয়, এর অনেক ধরনের বৈশিষ্ট্য রয়েছে। চোখ এবং চোখের দৃষ্টি নিয়ে সহজ কয়েকটা বৈশিষ্ট্য এখানে আলোচনা করা হলো।
(a) চোখের সামনে কোনো বস্তু রাখা হলে রেটিনাতে তার প্রতিবিম্ব তৈরি হয় এবং আমরা বস্তুটি দেখতে পাই। বস্তুটি চোখের সামনে থেকে সরিয়ে নেওয়ার সাথে সাথে কিন্তু বস্তুটি দেখার অনুভূতি চলে যায় না, সেটি আরও 0.01 সেকেন্ডের মতো থেকে যায়। এই সময়কে দর্শনানুভূতির স্থায়িত্বকাল বলে। দর্শনানুভূতির স্থায়িত্বকালের কারণে আমরা চলচ্চিত্র বা ভিডিও দেখার অনুভূতি পাই ।
(b) আমাদের দুটি চোখ সামনে (পাখিদের মতো দুই পাশে নয় তবে প্যাঁচার কথা আলাদা, প্যাঁচার চোখ মানুষের মতো সামনে), তাই আমরা একই সাথে দুই চোখে দুটি প্রতিবিম্ব দেখি। আমাদের মস্তিষ্ক এই দুটি প্রতিবিম্বকে উপস্থাপন করে আমাদেরকে দূরত্বের অনুভূতি দেয়।
(c) তোমরা এর মাঝে জেনেছ যে আমাদের রেটিনাতে একটা বস্তুর উল্টো প্রতিবিম্ব পড়লেও আমরা কস্তুটিকে সোজা দেখার অনুভূতি পাই কারণ দেখার অনুভুতিটি চোখ থেকে আসে না, সেটি আসে মস্তিক্ষ থেকে। চোখের রেটিনাতে যে প্রতিবিম্ব পড়ে সেটি থেকে আলোর সংকেত অপটিক নার্ভে করে মস্তিকে যায়, মস্তিক সেটাকে বিশ্লেষণ করে আমাদেরকে দেখার অনুভূতি দেয়।
তোমরা সবাই জানো আমরা যখন কোনো কিছু দেখি তখন তার উপর থেকে প্রতিফলিত হয়ে আলো আমাদের চোখে এসে পড়ে। চোখের কর্নিয়া এবং লেন্স মিলে সেই আলোটির একটি নিখুঁত প্রতিবিম্ব তৈরি করে আমাদের চোখের রেটিনার উপর ফেলে। আমাদের রেটিনাতে আলো সংবেদী দুই ধরনের কোষ রয়েছে। এক ধরনের কোষের নাম “রড" অন্য ধরনের কোষের নাম “কোন”। রড জাতীয় কোষগুলো অত্যন্ত সংবেদনশীল এবং খুব অল্প আলোতে কাজ করতে পারে কিন্তু সেগুলো রং শনাক করতে পারে না। সে জন্য জোছনার মৃদু আলোতে আমরা আবছাভাবে সবকিছু দেখতে পেলেও তাদের রং দেখতে পারি না। যদি আলোর তীব্রতা বেশি হয় তখন চোখের রেটিনার কোনগুলো কাজ করতে পারে। এই কোনগুলো রং সংবেদী, তাই আমরা তখন যদি কোনো কিছু দেখি তার রংগুলো দেখতে পারি।
তোমরা টেলিভিশনের কিংবা কম্পিউটারের মনিটরে কিংবা বইপুস্তকের রঙিন ছবি যদি খুব সুক্ষ্মভাবে দেখতে পারো তাহলে দেখবে সেখানকার রংগুলো আসে লাল, সবুজ এবং নীল রঙের সুক্ষ্ম বিন্দু দিয়ে অর্থাৎ এই তিনটি রং প্রয়োজনীয় তীব্রতা দিয়ে অন্য সব রং তৈরি করা যায়।
Read more