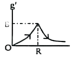Summary
৭.১ সূচনা
গ্রহ-নক্ষত্রের প্রকৃতি ও গতিবিধি সম্পর্কে পুরাতনকাল থেকেই বিজ্ঞানীদের কৌতূহল ছিল। টাইকো ব্র ও জোহান্স কেপলার গ্রহ-নক্ষত্রের গতি সম্পর্কিত গুরুত্বপূর্ণ অবদান রাখেন। কেপলার প্রথমে বুঝতে পারেন যে, গ্রহগুলো সূর্যকে কেন্দ্র করে ঘুরছে, কিন্তু এর পেছনের কারণ জানতেন না। 1681 সালে স্যার আইজাক নিউটন "মহাকর্ষ সূত্র" আবিষ্কার করে এই সমস্যা সমাধান করেন, যখন তিনি একটি আপেল পড়ার ঘটনা থেকে মহাকর্ষ ও অভিকর্ষের ধারণা প্রাপ্ত হন। এ অধ্যায়ে মহাকর্ষ, অভিকর্ষ, নিউটনের মহাকর্ষ সূত্র, কেপলারের সূত্র, এবং গ্রহের গতির আলোচনা করা হবে।
৭.২ মহাকর্ষ ও অভিকর্ষ
নিউটন আবিষ্কার করেন, মহাবিশ্বের কোন দুটি বস্তু বা কণার মধ্যে একটি পারস্পরিক আকর্ষণ রয়েছে, যা কখনও মহাকর্ষ ও কখনও অভিকর্ষ নামে পরিচিত।
- মহাকর্ষ: নভোমণ্ডলে অবস্থিত দুটি বস্তু বা কণার মধ্যকার আকর্ষণ বল। উদাহরণ: সূর্য ও চন্দ্রের মধ্যে।
- অভিকর্ষ: পৃথিবী ও অন্য একটি বস্তু বা কণার মধ্যকার আকর্ষণ বল। উদাহরণ: পৃথিবী ও চন্দ্রের মধ্যে বা পৃথিবী ও একটি আপেলের মধ্যে।
৭.১ সূচনা
Introduction
গ্রহ-নক্ষত্রের প্রকৃতি, স্বরুপ, গতিবিধি ইত্যাদি সম্পর্কে প্রাচীনকাল থেকেই বিজ্ঞানীদের অপরিসীম কৌতূহল ছিল। বিখ্যাত জ্যোতির্বিদ টাইকো ব্র (Tycho Brahe), জোহান্স কেপলার (Johannes Kepler) গ্রহ, নক্ষত্রের গতিবিধি সম্পর্কে উল্লেখযোগ্য অবদান রাখেন। কেপলার প্রথম উপলব্ধি করেন যে গ্রহগুলো কোন এক বলের প্রভাবে সূর্যকে কেন্দ্র করে অবিরত ঘুরছে। কিন্তু কি ধরনের বল ক্রিয়াশীল তা সঠিকভাবে বোঝাতে সমর্থ হননি। 1681 খ্রিস্টাব্দে মহাবিজ্ঞানী স্যার আইজাক নিউটন (Sir Isaac Newton) প্রথম “মহাকর্ষ সূত্র' আবিষ্কার করে এ সমস্যার সমাধান করেন। কথিত আছে, নিউটন তাঁর গৃহ-সংলগ্ন বাগানে একটি আপেল গাছের নিচে বসে বই পড়ছিলেন। এমন সময় একটি আপেল তাঁর নিকটে মাটিতে পড়ে। তিনি ভাবলেন গাছের উপরে ফাঁকা, নিচে ফাঁকা, ডানে ফাঁকা এবং বামেও ফাঁকা। আপেল ফল মাটিতে পড়ল কেন ? এই 'কেন' এর উদ্ঘাটন করতে গিয়ে তিনি মহাকর্ষ (Gravitation) এবং অভিকর্ষ (Gravity) আবিষ্কার করেন এবং সূর্যের চারদিকে গ্রহ-উপগ্রহের আবর্তনের কারণ ব্যাখ্যা করেন। এ অধ্যায়ে আমরা মহাকর্ষ, অভিকর্ষ, নিউটনের মহাকর্ষ সূত্র, অভিকর্ষজ ত্বরণ, মুক্তি বেগ, কেপলারের সূত্র, গ্রহের গতি ইত্যাদি আলোচনা করব।
৭.২ মহাকর্ষ ও অভিকর্ষ
Gravitation and gravity
বিখ্যাত বিজ্ঞানী স্যার আইজাক নিউটন আবিষ্কার করেন যে এ মহাবিশ্বের যে কোন দুটি বস্তু বা বস্তু কণার মধ্যে একটি পারস্পরিক আকর্ষণ রয়েছে। দুটি বস্তু বা বস্তুকণার মধ্যকার এই পারস্পরিক আকর্ষণ বলকে কখনও মহাকর্ষ আবার কখনও অভিকর্ষ বলা হয়।
এ দুটি বলের মধ্যে পার্থক্য রয়েছে। তাহলে প্রশ্ন জাগে মহাকর্ষ ও অভিকর্ষ কি ? এদের সংজ্ঞা নিম্নে দেয়া হল :
মহাকর্ষ : “নভোমণ্ডলে অবস্থিত দুটি বস্তু বা বস্তুকণার মধ্যকার পারস্পরিক আকর্ষণ বলকে মহাকর্ষ বলে।
অভিকর্ষ : “পৃথিবী এবং অন্য একটি বস্তু বা বস্তুকণার মধ্যকার আকর্ষণ বলকে অভিকর্ষ বা মাধ্যাকর্ষণ বলে।”
উদাহরণ :
সূর্য এবং চন্দ্রের মধ্যকার পারস্পরিক আকর্ষণ বলের নাম মহাকর্ষ, অপর পক্ষে পৃথিবী ও চন্দ্রের মধ্যকার পারস্পরিক আকর্ষণ বলই অভিকর্ষ। আরও সোজা ভাষায় বলা যায় পৃথিবী এবং আম গাছের একটি আমের মধ্যকার যে আকর্ষণ বল তা অভিকর্ষ। কিন্তু একই আম গাছের দুটি আমের মধ্যকার পারস্পরিক আকর্ষণ বলের নাম মহাকর্ষ।
# বহুনির্বাচনী প্রশ্ন
i ও ii
i ও iii
ii ও iii
i, ii ও ill
আমরা সর্বদা দেখি যে, কোনো বস্তুকে উপর থেকে নিচে ছেড়ে দিলে তা সরাসরি নিচে পৌঁছায়। আমরা কি কখনও ভেবে দেখেছি? একই সাথে ভারী এবং হালকা বস্তুকে একই স্থান থেকে নিচে ছেড়ে দিলে। তারা কি একই সাথে একই সময়ে ভূপৃষ্ঠে পৌঁছায়? আমরা দেখি যে, ভারী বস্তু ও হালকা বস্তু একই উচ্চতা থেকে পড়তে দিলে ভারী বস্তু আগে পৌছায়।
যেহেতু বস্তুর উপর ক্রিয়াশীল অভিকর্ষজ তরণ বস্তুর ভরের উপর নির্ভর করে না, তাই ভর ও বস্তুর উপর ক্রিয়াশীল অভিকর্ষজ ত্বরণ একই। সুতরাং এদের একই সময়ে মাটিতে পৌঁছানোর কথা বস্তুর পতনের সময়ের যে পার্থক্য পাওয়া যায় তা বায়ুর বাধার জন্য।
গ্যালিলিও উঁচু মান মন্দিরের ছাদ থেকে একই রকমের ভারী বস্তু ফেলে দেখান যে, এরা প্রায় একই সময়ে মাটিতে পৌছায়। বাতাসের বাধা না থাকলে তারা একত্রেই মাটিতে পৌছাত। বাতাসের মধ্যে বস্তুদ্বয় থাকার জন্য এদের ওজনের বিপরীত দিকে বাতাসের বাধাগ্রস্ত করে। ভারী বস্তুর চেয়ে হালকা কাগজের ওপর প্রবতা বা ঊর্ধ্বমুখী বল বেশি হওয়ায় কাগজ দেরিতে মাটিতে পৌছায়।
যেহেতু বস্তুর ওপর ক্রিয়াশীল অভিকর্ষজ ত্বরণ বস্তুর ভরের ওপর নির্ভর করে না, তাই ভারী বস্তু ও কাগজের ওপর ক্রিয়াশীল অভিকর্ষজ ত্বরণ একই।
পড়ন্ত বস্তু সম্পর্কে গ্যালিলিও তিনটি সূত্র দিয়েছেন। এগুলোকে পড়ন্ত বস্তুর ক্ষেত্রে গ্যালিলিওর সূত্র বলে।
যা স্থির অবস্থা থেকে বিনা বাধায় পড়ন্ত বস্তুর ক্ষেত্রে প্রযোজ্য।
সূত্রগুলো নিম্নে প্রদত্ত হলো
১ম সূত্র :
বায়ুশূন্য স্থানে বা বাধাহীন পথে সকল বস্তুই নিশ্চল অবস্থা হতে যাত্রা করে সমান দ্রুততায় নিচে নামে অর্থাৎ সমান সময়ে সমান দূরত্ব অতিক্রম করে।
ব্যাখ্যা : ছোট, বড় ও বিভিন্ন ওজনের কতকগুলো বস্তু একই উচ্চতা হতে ও স্লিাকথা হতে ছেড়ে দিলে রাধাহীন পথে তারা সমান দ্রুততায় অর্থাৎ ত্বরণে গতিশীল থাকবে এবং একই সময়ে মাটিতে পড়বে।
২য় সূত্র :
বাধাহীন পথে পড়ন্ত বস্তুর নির্দিষ্ট সময়ে প্রাপ্ত বেগ ঐ সময়ের সমানুপাতিক। কোনো পড়ন্ত বস্তু সময়ে বেগ প্রাপ্ত হলে, গাণিতিকভাবে লেখা যায়, v t ।
ব্যাখ্যা : অভিকর্ষের টানে স্থিরাবস্থা হতে বাধাহীন পথে নিচের দিকে পড়বার সময় কোনো বস্তুর বেগ যদি এক সেকেন্ড পরে v হয় তবে তার বেগ দুই সেকেন্ড পরে V × 2, তিন সেকেন্ড পরে V× 3 ইত্যাদি হবে। সাধারণভাবে বলা যায় যে, কোনো একটি পড়ন্ত বস্তুর বেগ t1 ও t2 সময়ে যথাক্রমে v1 ও v2
৩য় সূত্রে
বাধাহীন পথে পড়ন্ত বস্তুর নির্দিষ্ট সময়ে অতিক্রান্ত দূরত্ব ঐ সময়ের বর্গের সমানুপাতিক।
কোনো পড়ন্ত বস্তু t সময়ে h দুরত্ব অতিক্রম করলে গাণিতিক নিয়মে লেখা যায়-
ব্যাখ্যা : অভিকর্ষের টানে স্থিতাবস্থা হতে বাধাহীন পথে নিচের দিকে পড়বার সময় কোনো বস্তু যদি প্রথম সেকেন্ডে h দূরত্ব অতিক্রম করে তবে বস্তুটি দুই সেকেন্ডে 22 × h, তিন সেকেন্ডে 32 × h ইত্যাদি দূরত্ব অতিক্রম করবে।
# বহুনির্বাচনী প্রশ্ন
1687 খ্রিস্টাব্দে বিখ্যাত বিজ্ঞানী স্যার আইজ্যাক নিউটন আপেল পতন এবং গ্রহ-উপগ্রহের গতি পর্যবেক্ষণ করে মহাকর্ষের যে সূত্র আবিষ্কার করেন তা নিম্নোক্তভাবে সংজ্ঞায়িত করা যায় :
“মহাবিশ্বের যে কোন দুটি বস্তুকণা পরস্পরকে আকর্ষণ করে। এই আকর্ষণ বল বস্তু দুটির ভরের গুণফলের সমানুপাতিক, তাদের দূরত্বের বর্গের ব্যস্তানুপাতিক এবং বস্তু দুটির সংযোগকারী সরলরেখা বরাবর ক্রিয়াশীল । "
ব্যাখ্যা ঃ
নিউটনের মহাকর্ষ সূত্র বিশ্লেষণ করলে দেখা যাবে এই সূত্রে তিনটি অংশ রয়েছে। দুটি অংশ বলের পরিমাণ নির্দেশ করে আর একটি অংশ বলের প্রকৃতি সম্বন্ধীয়।
বলের পরিমাপ : মনে করি দুটি বস্তুকণার ভর যথাক্রমে m1 ও m2 এবং তাদের মধ্যবর্তী দূরত্ব d [চিত্র ৭.১]। যদি তাদের মধ্যে আকর্ষণ বল F হয়, তবে মহাকর্ষ সূত্র অনুসারে
(i)
(ii)
(i) ও (ii)-কে যুক্ত করে পাই,
এখানে, G একটি সমানুপাতিক ধ্রুবক। এই ধ্রুবককে মহাকর্ষীয় ধ্রুবক (Gravitational constant) বা বিশ্বজনীন মহাকর্ষীয় ধ্রুবক (Universal gravitational constant) বলা হয়। G-কে বিশ্বজনীন ধ্রুবক বলা হয় কারণ G-এর মান বস্তুকণা দুটির মধ্যবর্তী মাধ্যমের প্রকৃতির ওপর যেমন—প্রবেশ্যতা (permeability), প্রবণতা (susceptibility), দিকদর্শিতা (directivity) এবং বস্তুকণা দুটির ভৌত অবস্থার উপর নির্ভর করে না।
বলের প্রকৃতি :
মহাকর্ষ বল দুটি বস্তুর মধ্যকার পারস্পরিক আকর্ষণ বল। দুটি চার্জিত বস্তু কিংবা দুটি চুম্বক পরস্পরকে আকর্ষণ করে যখন চার্জ দুটি বিপরীতধর্মী অর্থাৎ একটি ধনাত্মক ও অপরটি ঋণাত্মক হয় এবং বিকর্ষণ করে যখন চার্জ দুটি সমধর্মী হয়। চুম্বকের ক্ষেত্রে আকর্ষণ হয় যখন চুম্বকদ্বয়ের বিপরীত মেরু কাছাকাছি আসে এবং বিকর্ষণ করে যখন মেরুদ্বয় সমধর্মী হয়। কিন্তু মহাকর্ষ শুধুমাত্র আকর্ষণ বল। মহাকর্ষ বল বস্তু দুটির সংযোগ সরলরেখা বরাধর ক্রিয়া করে। এছাড়া মহাকর্ষ বল মাধ্যমের উপর নির্ভর করে না। মাধ্যম যাই হোক না এই বলের কোন পরিবর্তন হয় না।
# বহুনির্বাচনী প্রশ্ন
মহাকর্ষ সূত্রকে ভেক্টর রাশির দ্বারা নিম্নলিখিতভাবে লেখা যায় :
এখানে F21 হচ্ছে দ্বিতীয় বস্তুর উপর প্রথম বস্তুর সদিক বল (আকর্ষণ) হচ্ছে প্রথম বস্তু হতে দ্বিতীয় বস্তুর সদিক দূরত্ব।
যেহেতু প্রথম বস্তু আকর্ষণ করে দ্বিতীয় বস্তুকে নিজের দিকে টানছে অর্থাৎ এবং দিক এর বিপরীত, সুতরাং উপরোক্ত সমীকরণে ঋণাত্মক চিহ্ন ব্যবহৃত হয়েছে। কিন্তু মহাকর্ষ বলের মান সূচক। সুতরাং ঋণাত্মক চিহ্ন ব্যবহৃত হয়নি।
৭.৩ মহাকর্ষীয় ধ্রুবকের সংজ্ঞা, একক এবং মাত্রা
সমীকরণ (1) হতে পাই,
মনে করি দুটি বস্তুকণার প্রত্যেকটির ভর এক একক এবং তাদের মধ্যবর্তী দূরত্বও এক একক অর্থাৎ
m1 = 1 একক, m2 = 1 একক এবং d = 1 একক।
সুতরাং, মহাকর্ষীয় ধ্রুবকের সংজ্ঞা হিসেবে বলা যায়— “একক ভরবিশিষ্ট দুটি বস্তুকণা একক দূরত্বে থেকে যে পরিমাণ বল দ্বারা পরস্পরকে আকর্ষণ করে তার সংখ্যাগত মানকে মহাকর্ষীয় ধ্রুবক বলে।”
যদি বলা হয় “G = 6.67 x 10-11 এস. আই. একক” – এর অর্থ এই যে, দুটি বস্তুকণার প্রত্যেকটির ভর 1 কিলোগ্রাম এবং তাদের মধ্যবর্তী দূরত্ব 1 মিটার হলে তারা পরস্পরকে 6.67 × 10-11 নিউটন বল দ্বারা আকর্ষণ করবে।
একক :
এস. আই. পদ্ধতিতে F-এর একক নিউটন, d-এর একক মিটার এবং m-এর একক কিলোগ্রাম।
তা হলে উপরের সমীকরণ (2)-এ বিভিন্ন রাশির একক বসালে, এম. কে. এস. ও এস. আই. পদ্ধতিতে G-এর_
একক নিউটন-মিটার২/ কিলোগ্রাম২ (N-m2. kg-2)।
মাত্রা সমীকরণ :
সমীকরণ (1) অনুসারে G-এর মাত্রা সমীকরণ,
৭.৪ মহাকর্ষীয় ধ্রুবক কি বিশ্বজনীন ?
G-কে বিশ্বজনীন বা সর্বজনীন ধ্রুবক বলা হয়। কারণ G-এর মান বস্তুকণা দুটির মধ্যবর্তী মাধ্যমের উপর কিংবা বস্তুকণা দুটির ভৌত অবস্থার উপর নির্ভর করে না। পদার্থবিজ্ঞানে অনেক ধ্রুবক রয়েছে যাদের ে কোনটি মাধ্যমের প্রকৃতির উপর নির্ভর করে, বস্তুর অবস্থার উপর (যেমন তাপমাত্রা, চাপ ইত্যাদি) নির্ভর করে, বস্তুর প্রকৃতির উপর নির্ভর করে। কিন্তু মহাকর্ষীয় ধ্রুবক এমন একটি ধ্রুবক যার মান সর্বত্র এবং সব অবস্থায় একই থাকে, কোন পরিবর্তন হয় না। এই কারণেই এই ধ্রুবককে বিশ্বজনীন ধ্রুবক বলে।
# বহুনির্বাচনী প্রশ্ন
মহাকর্ষীয় ধ্রুবকের মান নির্ণয়ের জন্য অনেকগুলো পদ্ধতি আছে। তবে এখানে আমরা ক্যাভেন্ডিসের পদ্ধতি আলোচনা করব ।
ক্যাভেন্ডিসের পদ্ধতি (Cavendish's method) :
1798 খ্রিস্টাব্দে বিজ্ঞানী ক্যাভেন্ডিস মহাকর্ষীয় ধ্রুবকের মান নির্ণয়ের জন্য একটি ব্যবর্ত তুলা পদ্ধতি উদ্ভাবন করেন। তাঁর নাম অনুসারে এই পদ্ধতিকে ক্যাভেন্ডিসের পদ্ধতি বলা হয়।
যন্ত্রের বর্ণনা:
এই যন্ত্রে সীসার তৈরি চারটি গোলক (A, B, C ও D) আছে। এদের মধ্যে A ও B ছোট এবং C ও D দুটি বড় গোলক[চিত্র ৭.২] । C এবং D একটি অনুভূমিক দণ্ড PQ-এর দু'প্রান্ত হতে ঝুলান হয়েছে। দণ্ডটি একটি উল্লম্ব অক্ষ XX'-এর সাথে যুক্ত থাকে। এই অক্ষ একটি চাকা W-এর সঙ্গে যুক্ত থাকে। চাকাটি বাহির হতে ঘুরানোর ব্যবস্থা থাকে। এর কিছুটা নিচে একই অক্ষে একটি ব্যবর্তন শীর্ষ ( torsion head) H হতে ব্যবর্তন তারের (T) সাহায্যে একটি হাল্কা দণ্ড RS ঝুলান আছে। RS-এর দু'প্রান্ত হতে দুটি ছোট সমান ভরের গোলক A ও B ঝুলান আছে। A, B এবং C, D একই অনুভূমিক তলে থাকে। T ব্যবর্তন তারের সাথে একটি দর্পণ (E) লাগানো থাকে। একটি আলোক উৎস (L) হতে দর্পণের উপর আলোক রশ্মি আপতিত করানো হয় এবং প্রতিফলিত রশ্মি একটি স্কেলের (S) উপর নিক্ষেপ করানো হয়। স্কেলের উপর প্রতিফলিত আলোক রশ্মির সরণ পরিমাপ করে ব্যবর্তন তারের মোচড় কোণ পরিমাপ করা হয়।
কার্যপদ্ধতি :
প্রথমে চাকা W-এর সাহায্যে PQ দণ্ডকে ঘুরিয়ে বড় গোলক দুটিকে দূরে সরিয়ে নেয়া হয় যাতে ছোট গোলকের উপরে প্রভাব না পড়ে। এই অবস্থায় স্কেলে দর্পণ E হতে প্রতিফলিত রশ্মির অবস্থানের পাঠ নেয়া হয়। এরপর বড় গোলক দুটিকে ছোট গোলক দুটির কাছাকাছি অবস্থানে আনা হয়। প্রত্যেক বড় গোলক (C বা D) তার নিকটে অবস্থিত ছোট গোলকের (A বা B) উপর একটি আকর্ষণ বল প্রয়োগ করে। সমান ও বিপরীতমুখী এই দুটি বল একটি বিক্ষেপী দ্বন্দ্বের (deflecting couple) সৃষ্টি করে যার ফলে RS দন্ডটি একটি ক্ষুদ্র কোণে ঘুরতে বাধ্য হয়। সুতরাং ব্যবর্তন তারে পাক পড়ে। তারটি এর স্থিতিস্থাপকতা ধর্মের জন্য বিপরীতমুখী প্রত্যায়নী দ্বন্দ্বের (restoring couple) সৃষ্টি করে দণ্ডটিকে পূর্বের অবস্থানে ফিরিয়ে নিতে সচেষ্ট হয়। দুটি পরস্পর বিপরীতমুখী দ্বন্দ্বের ক্রিয়ায় দণ্ডটি একটি সাম্য অবস্থানে আসে। এই অবস্থায় স্কেলে দর্পণ হতে প্রতিফলিত রশ্মির নতুন অবস্থানের পাঠ নেয়া হয়। প্রথম পাঠ ও দ্বিতীয় পাঠের পার্থক্য হতে দণ্ডের কৌণিক বিক্ষেপ নির্ণয় করা হয়। এরপর বড় গোলক দুটির অবস্থান [চিত্র ৭.৩] পূর্ব অবস্থান (K, m)-এর বিপরীত পার্শ্বে করা হয়।[চিত্রে K', m´ অবস্থান]। এভাবে ঘুরিয়ে দণ্ডের কৌণিক বিক্ষেপের মান বের করা হয়। পরিশেষে এই দুটি বিক্ষেপের গড় মান নির্ণয় করা যায় ।
হিসাব বা গণনা :
মনে করি,
প্রত্যেকটি বড় গোলকের ভর =M
প্রত্যেকটি ছোট গোলকের ভর = m
RS দণ্ডের দৈর্ঘ্য = 2l
দণ্ডটির সাম্যাবস্থায় বড় ও ছোট্ গোলকের কেন্দ্রবিন্দুর মধ্যবর্তী দূরত্ব = d
A ও C গোলকের মধ্যকার আকর্ষণ বল,
B এবং D গোলক দুটির মধ্যে অনুরূপ আকর্ষণ বল বিদ্যমান আছে। এই দুটি সমান ও বিপরীতমুখী বল একটি দ্বন্দ্বের সৃষ্টি করে ।
অতএব, ব্যবর্তন শীর্ষ H সাপেক্ষে বিক্ষেপী দ্বন্দ্বের মোমেন্ট
দন্ডটি যদি '' কোণে বিচ্যুত হয় তাহলে মোচড়ের জন্য ব্যবর্তন তারে (T)
প্রত্যায়নী দ্বন্দ্বের মোমেন্ট =
এখানে = প্রতি ডিগ্রী বিক্ষেপের জন্য প্রত্যায়নী দ্বন্দ্বের মোমেন্ট।
সাম্যাবস্থায়, বিক্ষেপী দ্বন্দ্বের মোমেন্ট = প্রত্যায়নী দ্বন্দ্বের মোমেন্ট।
বা,
:-
এখন , d, 2l, M এবং m পরীক্ষা হতে জানা যায়। -এর মান জানা থাকলেই G-এর মান পাওয়া যাবে।
-এর মান নির্ণয় করার জন্য বড় দুটি গোলককে সরিয়ে ফেলি। তারপর ছোট দুটি গোলকসহ RS দণ্ডকে ব্যবর্তন তার T-এর সাপেক্ষে ব্যবর্তন দোলনে দোলাই এবং দোলনকাল নির্ণয় করি। যদি দোলনকাল T হয়, তবে,
বা,
সমীকরণ (6) হতে পাই,
সমীকরণ (7)-এর ডান পাশের সকল রাশির মান জানা থাকায় G-এর মান বের করা যায়। বিজ্ঞানী ক্যাভেন্ডিস এ পরীক্ষা বারবার পুনরাবৃত্তি করেন এবং G-এর গড় মান বের করেন। এর লব্ধ মান হল
G = (6.754 0.41) × 10-11 N-m² kg-2
# বহুনির্বাচনী প্রশ্ন
1:1
1:2
2:1
4:1
নিউটনের গতির সূত্র অনুসারে বস্তুর উপর বল প্রয়োগ করলে ত্বরণ সৃষ্টি হয়। অভিকর্ষও একটি বল। এই বল কোন একটি বস্তুর উপর ক্রিয়া করে ত্বরণ সৃষ্টি করবে। অতএব, বস্তুতে অভিকর্ষ বল কর্তৃক যে ত্বরণ উৎপন্ন হয় তাকে অভিকর্ষজ ত্বরণ বলে। অথবা কোন স্থানে অভিকর্ষের টানে মুক্তভাবে পড়ন্ত বস্তুর বেগ যে হারে বৃদ্ধি পায় তাকে ঐ স্থানের অভিকর্ষজ বা অভিকর্ষীয় ত্বরণ বলে। একে 'g' দ্বারা প্রকাশ করা হয়।
পরীক্ষার সাহায্যে জানা গেছে, বাধাহীন পথে ও একই স্থান হতে সকল বস্তু সমত্বরণে পৃথিবীর কেন্দ্রের দিকে পতিত হয়। স্থানভেদে এই ত্বরণের মান বিভিন্ন। সুতরাং অভিকর্ষজ ত্বরণ বস্তু নিরপেক্ষ, স্থান নিরপেক্ষ নয়।
এর একক এম. কে. এস. ও আন্তর্জাতিক SI পদ্ধতিতে মিটার/সে.২। এর মাত্রা সমীকরণ [LT-2]।
অভিকর্ষজ ত্বরণের সমীকরণ
(Equation of acceleration due to gravity)
মনে করি ‘m’ ভরবিশিষ্ট একটি বস্তুকণা পৃথিবী পৃষ্ঠে অবস্থিত এবং পৃথিবী একটি গোলাকার বস্তু [চিত্র ৭.৪ ]। যদি পৃথিবীর ভর ‘M' এবং ব্যাসার্ধ 'R' হয়, তবে নিউটনের মহাকর্ষ সূত্র হতে আমরা পাই,
পুনরায়, নিউটনের গতির দ্বিতীয় সূত্র হতে আমরা পাই,
বল = ভর x ত্বরণ
অভিকর্ষীয় বল = বস্তুর ভর × অভিকর্ষজ ত্বরণ। অর্থাৎ,
সমীকরণ (8) এবং সমীকরণ (9) হতে আমরা পাই,
বা,
এটিই হল ভূ-পৃষ্ঠে অভিকর্ষজ ত্বরণের সমীকরণ। সমীকরণ অনুসারে অভিকর্ষজ ত্বরণ ৪ বস্তুর ভর m-এর
উপর নির্ভর করে না। আবার, আমরা জানি G এবং M ধ্রুব রাশি। অতএব ভূ-পৃষ্ঠের কোন স্থানে ‘g ’-এর মান ভূ-কেন্দ্র হতে ঐ স্থানের দূরত্বের উপর নির্ভর করে। এটি হতে এই সিদ্ধান্তে উপনীত হওয়া যায় যে, ভূ-পৃষ্ঠের কোন একটি স্থানে g-এর মান নির্দিষ্ট, কিন্তু স্থানভেদে এর পরিবর্তন ঘটে।
পৃথিবীর ভর M= 5.983 × 1024 kg এবং ব্যাসার্ধ R = 6.36 x 106m ধরে উপরের সমীকরণ অনুসারে ভূ-পৃষ্ঠের g-এর মান হয়,
৭.৭ অভিকর্ষজ ত্বরণ 'g'-এর তারতম্য
Variation of acceleration due to gravity, 'g'
অভিকর্ষজ ত্বরণ ধ্রুব নয়। তিনটি কারণে এর তারতম্য ঘটে :
(১) উচ্চতার ক্রিয়া (Altitude effect),
(২) অক্ষাংশ ক্রিয়া (Latitude effect) এবং
(৩) পৃথিবীর ঘূর্ণন ক্রিয়া (Rotational effect of the earth)।
নিম্নে এই বিষয়গুলো আলোচনা করা হল :
(১) উচ্চতার ক্রিয়া :
পৃথিবীর কেন্দ্র হতে কোন স্থানের দূরত্বের তারতম্য ভেদে অভিকর্ষজ ত্বরণ 'g'-এর মানের পরিবর্তন ঘটে। এটি আলোচনা করতে হলে তিনটি বিষয় আলোচনা করতে হয়; যথা—
(ক) কোন বস্তু পৃথিবী পৃষ্ঠে অবস্থিত :
কোন বস্তু যদি ‘M’ ভর এবং ‘R’ ব্যাসার্ধবিশিষ্ট পৃথিবী পৃষ্ঠে অবস্থান করে [ চিত্র ৭.৫ ] তবে ঐ বস্তুর উপর তথা ভূ-পৃষ্ঠে,
এখানে, p = পৃথিবীর উপাদানের গড় ঘনত্ব ও = পৃথিবীর আয়তন ।
(খ) কোন বস্তু পৃথিবী পৃষ্ঠ হতে উপরে অবস্থিত :
মনে করি M পৃথিবীর ভর এবং R তার ব্যাসার্ধ। যদি বস্তু পৃথিবী পৃষ্ঠ হতে h উচ্চতায় উপরে অবস্থান করে। [চিত্র ৭.৬] তবে ঐ বস্তুর উপর তথা ভূ-পৃষ্ঠ হতে h উচ্চতায় অভিকর্ষীয় ত্বরণ,
সমীকরণ (11) অপেক্ষা সমীকরণ (13)-এ হরের মান বেশি। কাজেই ভাগফল অর্থাৎ অভিকর্ষীয় ত্বরণ-এর মান কম হবে। অতএব পৃথিবী পৃষ্ঠ অপেক্ষা উপরে অভিকর্ষীয় ত্বরণ-এর মান কম হবে এবং দূরত্বের বর্গের ব্যস্তানুপাতে পরিবর্তিত হবে। সুতরাং দূরত্ব বাড়লে অভিকর্ষীয় ত্বরণ-এর মান কমবে এবং দূরত্ব কমলে অভিকর্ষীয় ত্বরণ-এর মান বাড়বে। এই কারণে পাহাড়ের উপর অভিকর্ষীয় ত্বরণ-এর মান পৃথিবী পৃষ্ঠে অভিকর্ষীয় ত্বরণ-এর মান অপেক্ষা কম হয়।
সমীকরণ (13)-কে সমীকরণ (10) দ্বারা ভাগ করে পাওয়া যায়,
হলে,
বা,
অর্থাৎ,
(গ) কোন বস্তু পৃথিবী পৃষ্ঠ হতে নিচে অবস্থিত :
মনে করি পৃথিবী পৃষ্ঠ হতে h দূরত্ব নিচে B বিন্দুতে কোন বস্তু আছে এবং ঐ স্থানে অভিকর্ষীয় ত্বরণ gd [চিত্র ৭.৭]। B বিন্দুতে অবস্থিত যে কোন বস্তুর উপর ভূ-কেন্দ্র O-এর দিকে পৃথিবীর আকর্ষণ (R-h) ব্যাসার্ধবিশিষ্ট AB গোলকের আকর্ষণের সমান। এই গোলকের বাইরের অংশ বস্তুর উপর কার্যকর কোন আকর্ষণ প্রয়োগ করে না।
এখন AB গোলকের আয়তন
AB গোলকের ভর M´ ধরলে,
M = আয়তন × ঘনত্ব
বা, (15)
(16)
এখানে, একটি ধ্রুব রাশি।
উপরের সমীকরণ অনুসারে h-এর মান যত বাড়বে, (R-h )-এর মান তত কমবে। অতএব, যত পৃথিবীর ভেতরের দিক যাওয়া যাবে, অভিকর্ষীয় ত্বরণ-এর মান ততই কমবে অর্থাৎ ভূ-গর্ভে অভিকর্ষীয় ত্বরণ ভূ-কেন্দ্র হতে দূরত্বের সমানুপাতিক। এভাবে যেতে যেতে যদি ভূ-কেন্দ্রে পৌঁছা যায় তবে h-এর মান R-এর সমান হবে।
অতএব ভূ-কেন্দ্রে, gd = k (R - R)
বা, gd = 0
সুতরাং পৃথিবীর অভ্যন্তরে, যেমন কোন খনির ভেতরে g-এর মান ভূ-পৃষ্ঠে g-এর মান অপেক্ষা কম হয় ।
সিদ্ধান্ত : ভু-পৃষ্ঠের উপরে গেলে 'g'-এর মান কমে, আবার পৃথিবীর অভ্যন্তরে গেলে ‘g’-এর মান কমে। পৃথিবীর কেন্দ্রে কোন আকর্ষণ নেই। সুতরাং পৃথিবীর কেন্দ্রে 'g'-এর মান শূন্য এবং ভূ-পৃষ্ঠেই 'g'-এর মান সর্বাপেক্ষা বেশি।
উল্লেখ্য :
(i) সমীকরণ (11) হতে সরাসরি সমীকরণ (15) পাওয়া যায়।
(ii) সমীকরণ (15)-কে সমীকরণ (12) দ্বারা ভাগ করে পাওয়া যায়
অর্থাৎ, gd < g
(২) অক্ষাংশ ক্রিয়া—অক্ষাংশ পরিবর্তনে g-এর পরিবর্তন :
আমরা জানি পৃথিবী সম্পূর্ণ গোলাকার নয় ৷ এর আকৃতি উপগোলকীয় (spheroidal)। উত্তর ও দক্ষিণ মেরু কিছুটা চাপা এবং বিষুব-ব্যাস মেরু-ব্যাস অপেক্ষা প্রায় 43 km বৃহত্তর। সুতরাং বিষুব রেখায় অবস্থিত কোন বস্তু মেরু অঞ্চলে অবস্থিত বস্তু অপেক্ষা পৃথিবীর কেন্দ্র হতে অধিক দূরে অবস্থিত। অতএব বিষুব রেখায় অবস্থিত কোন বস্তুর উপর অভিকর্ষীয় আকর্ষণ বল মেরুতে অবস্থিত ঐ বস্তুর উপর অভিকর্ষীয় আকর্ষণ বল অপেক্ষা কম। সুতরাং বিষুব রেখায় 'g'-এর মান কম এবং মেরু অঞ্চলে 'g'-এর মান বেশি।
অতএব, বিষুব রেখা হতে ক্রমাগত মেরু অঞ্চলের দিকে অগ্রসর হলে 'g'-এর মান বাড়তে থাকবে এবং মেরুতে এর মান সর্বাপেক্ষা বেশি হবে।
(৩) পৃথিবীর ঘূর্ণনের ক্রিয়া—পৃথিবীর আহ্নিক গতির জন্য 'g'-এর মানের পরিবর্তন :
পৃথিবীর আহ্নিক বা দৈনিক গতির সাথে সাথে ভূ-পৃষ্ঠের যে কোন একটি বস্তু পৃথিবীর সাথে তার অক্ষের চর্তুদিকে সমান কৌণিক বেগে প্রদক্ষিণ করবে। এতে বস্তুটির উপর একটি কেন্দ্রমুখী বল প্রযুক্ত হবে এবং বস্তুটি তার বৃত্তাকার পথের ব্যাসার্ধ বরাবর ছিটকে বাইরের দিকে চলে যাবার চেষ্টা করবে। বস্তুর ওজনের কিছু অংশ এই কেন্দ্রবিমুখী বল প্রশমিত করতে ব্যয় হবে। ফলে অভিকর্ষীয় ত্বরণ ‘8' হ্রাস পাবে। আবার মেরু অঞ্চল অপেক্ষা বিষুব অঞ্চলে বস্তু অপেক্ষাকৃত বড় ব্যাসার্ধের বৃত্তাকার পথে ঘুরবে বলে কেন্দ্রবিমুখী বলও বৃদ্ধি পাবে। কাজেই g-এর মান মেরু অঞ্চলে সবচেয়ে বেশি এবং বিষুব অঞ্চলে সবচেয়ে কম হবে।
ধরা যাক m ভরের একটি বস্তু ভূ-পৃষ্ঠে (উত্তর) অক্ষাংশে P বিন্দুতে অবস্থান করে পৃথিবীর ঘূর্ণনে তার অক্ষ NS-এর চতুর্দিকে সমকৌণিক বেগে r ব্যাসার্ধবিশিষ্ট বৃত্তাকার পথে ঘুরছে [চিত্র : ৭.৮]। তা হলে বস্তুটির উপর তার বৃত্তাকার পথের স্পর্শক PT বরাবর সৃষ্ট কেন্দ্রবিমুখী বল,
PO বা ভূ-কেন্দ্র বরাবর বস্তুটির উপর পৃথিবীর আকর্ষণ,
OPD - বরাবর বা ভূ-কেন্দ্র হতে বাইরের দিকে কেন্দ্রবিমুখী বলের অংশক
T cosλ = m2r cos λ = m2 R cos2λ
বল দুটির লব্ধি,
(19)
P বিন্দুতে ভূ-কেন্দ্র অভিমুখে অভিকর্ষজ ত্বরণ হলে,
(20)
বিষুব অঞ্চলে,
আবার মেরু অঞ্চলে,
কাজেই, g-এর মান মের অঞ্চলে সবচেয়ে বেশি এবং বিষুব অঞ্চলে সবচেয়ে কম হবে।
এ সমস্ত আলোচনা এবং পরীক্ষালব্ধ ফলাফল হতে g-এর মান সম্পর্কে আমরা নিম্নলিখিত সিদ্ধান্তে উপনীত হতে পারি :
(১) পৃথিবীর পৃষ্ঠ হতে উপর দিকে উঠলে এর মান কমে।
(২) পৃথিবীর অভ্যন্তরে নামলে এর মান কমে।
(৩) বিষুবীয় অঞ্চল হতে মেরু অঞ্চলে অগ্রসর হলে এর মান বাড়ে।
(৪) ঘূর্ণনজনিত কারণে মেরু অঞ্চলে এর মান অল্প কমে, কিন্তু বিষুবীয় অঞ্চলে বেশি কমে।
(৫) মেরুতে g-এর মান = 9.832 ms-2 ; বিষুব অঞ্চলে g-এর মান = 9.780 ms-2 |
ঢাকায় g-এর মান = 9.7835 ms-2 ; রাজশাহীতে g-এর মান = 9.790 ms-2 |
(৬) ভূ-পৃষ্ঠে g-এর মান বিভিন্ন স্থানে বিভিন্ন বলে সমুদ্র পৃষ্ঠে এবং 45° অক্ষাংশের g-এর মানকে আদর্শ মান ধরা হয়। g-এর আদর্শ বা ব্যবহারিক মান = 9.81 ms-2।
(৭) g-এর মান জেনে পৃথিবীর গড় ঘনত্ব সম্বন্ধে একটি ধারণা লাভ করা যায়।
# বহুনির্বাচনী প্রশ্ন
মনে করি পৃথিবীর ভর = M, ব্যাসার্ধ = R এবং ভূ-পৃষ্ঠে অবস্থিত কোন বস্তুর ভর = m [চিত্র ৭.৯]। উক্ত বস্তুকে পৃথিবী যে বল দ্বারা আকর্ষণ করে তার মান,
(21)
পর্যবেক্ষণ স্থানে অভিকর্ষজ ত্বরণের মান g হলে বস্তুর ওজন,
(22)
এখন সমীকরণ (21) ও (22) হতে পাই,
বা,
বা, (23)
সমীকরণ (23)-এ, g = 9.8 ms-2, R = 6.37 × 106 m, G = 6.673 x 10-11 Nm-2kg-2 বসিয়ে,
ঘনত্ব :
মনে করি পৃথিবীর গড় ঘনত্ব =
ভর/আয়তন =
=5.5 x 103 kg m-3|
৭.৯ ভর এবং ওজন
Mass and weight
ভর : কোন একটি বস্তুতে মোট যে পরিমাণ পদার্থ আছে, তাকে তার ভর বলে।
একে সাধারণত ‘M’ বা 'm' দ্বারা প্রকাশ করা হয়। এটি একটি স্কেলার রাশি। বস্তুর ভর স্থান নিরপেক্ষ অর্থাৎ যে কোন স্থানে নেয়া হোক না কেন এর মান সর্বত্র স্থির থাকবে। বস্তুর ভর তার স্থিতি, গতি, তাপমাত্রা, চুম্বকত্ব বা তড়িতাবস্থা দ্বারা প্রভাবিত হয় না। সেজন্য ভর বস্তুর একটি স্বাভাবিক ধর্ম। এক্ষেত্রে উল্লেখ করা যেতে পারে যে কোন বস্তুর বেগ যদি আলোর বেগের কাছাকাছি হয় তা হলে বস্তুর ভরের পরিবর্তন দেখা যায়। বেগের সঙ্গে বস্তুর ভর পরিবর্তনের তত্ত্ব আইনস্টাইন (Einstein)-এর আপেক্ষিক তত্ত্বে (Theory of relativity) বিশদভাবে আলোচিত হয়েছে।
ওজন : কোন একটি বস্তু যে পরিমাণ বল দ্বারা পৃথিবীর কেন্দ্রের দিকে আকৃষ্ট হয় তাকে তার ওজন বা ভার বলে।
একে W দ্বারা প্রকাশ করা হয়। যেহেতু ওজন একটি বল ছাড়া আর কিছুই নয়, সুতরাং এটি একটি ভেক্টর রাশি এবং এর মান, w = ভর × অভিকর্ষজ ত্বরণ
বা, W = mg (25)
বিভিন্ন স্থানে g-এর মান বিভিন্ন বলে স্থানভেদে বস্তুর ওজন পরিবর্তিত হয়। অতএব বস্তুর ওজন স্থান নিরপেক্ষ নয়। এই প্রসংগে আরও বলা যায় যে, বস্তুর ওজন তার একটি মৌলিক বৈশিষ্ট্য নয়। বস্তুর ওজন থাকতে পারে, নাও থাকতে পারে। যেমন পৃথিবীর কেন্দ্রে বস্তুর কোন ওজন নেই।
৭.১০ বস্তুর ওজনের তারতম্য
Variation of weight of a body
আমরা জানি, ওজন W = mg ;
এখানে m = বস্তুর ভর এবং g =অভিকর্ষজ ত্বরণ।
বস্তুর ভর একটি ধ্রুব রাশি; সুতরাং কোন বস্তুর ওজন অভিকর্ষজ ত্বরণের উপর নির্ভরশীল। যে স্থানে অভিকর্ষজ ত্বরণ বেশি, সে স্থানে বস্তুর ওজনও বেশি। আর অভিকর্ষজ ত্বরণ যে স্থানে কম বস্তুর ওজনও সে স্থানে কম। উদাহরণস্বরূপ বলা যায়, মেরু অঞ্চলে অভিকর্ষজ ত্বরণ বেশি। সুতরাং মেরু অঞ্চলে বস্তুর ওজন বেশি। বিষুব অঞ্চলে অভিকর্ষজ ত্বরণ কম। অতএব বিষুব অঞ্চলে বস্তুর ওজনও কম। পৃথিবীর কেন্দ্রে অভিকর্ষজ ত্বরণ শূন্য। অতএব পৃথিবীর কেন্দ্রে বস্তুর কোন ওজন নেই।
৭.১১ মহাকর্ষীয় ধ্রুবক এবং অভিকর্ষজ ত্বরণের মধ্যে পার্থক্য
Distinction between gravitational constant and acceleration due to gravity
মহাকর্ষীয় ধ্রুবক এবং অভিকর্ষজ ত্বরণের মধ্যে নিম্নলিখিত পার্থক্য আছে ঃ
| মহাকর্ষীয় ধ্রুবক | অভিকর্ষজ ত্বরণ |
|---|---|
| ১। একক ভরবিশিষ্ট দুটি বস্তুর মধ্যবর্তী দূরত্ব এক একক হলে তাদেঁর পারস্পরিক আকর্ষণ বলকে মহাকর্ষীয় ধ্রুবক বলে। | ১। অভিকর্ষ বলের জন্য বস্তুতে যে ত্বরণ সৃষ্টি হয় তাকে অভিকর্ষজ ত্বরণ বলে। |
| ২। এর মাত্রা সমীকরণ | ২। এর মাত্রা সমীকরণ |
| ৩। একটি বিশ্বজনীন ধ্রুবক । | ৩। এটি একটি পরিবর্তনশীল রাশি। |
| ৪। এস. আই. পদ্ধতিতে এর মান 6.657 x 10-11 Nm2kg-2 | ৪। এস.আই.পদ্ধতিতে এর মান ভূ-পৃষ্ঠে 9.81 ms-2 |
| ৫। এর মান বস্তুর ভরের উপর বা ভূ-কেন্দ্র হতে বস্তুর দূরত্বের উপর নির্ভর করে | ৫। এর মান বস্তুর ভরের উপর নির্ভর করে না, কিন্তু দূরত্বের উপর নির্ভর করে না । |
| ৬। এটি একটি স্কেলার রাশি। | ৬। এটি একটি ভেক্টর রাশি |
# বহুনির্বাচনী প্রশ্ন
অভিকর্ষ কেন্দ্র :
আমরা জানি, কোন একটি বস্তু যে পরিমাণ বল দ্বারা পৃথিবীর কেন্দ্রের দিকে আকৃষ্ট হয়, তাকে বস্তুর ওজন বা ভার বলে।
বস্তুকে যেভাবেই রাখা হোক না কেন তার ওজন যে বিশেষ বিন্দুর মধ্য দিয়ে বস্তুর উপর সর্বদা ক্রিয়া করে ঐ বিন্দুকে বস্তুর অভিকর্ষ কেন্দ্র বলে। অভিকর্ষ কেন্দ্রের অপর নাম ভারকেন্দ্র।
মনে করি A একটি দৃঢ় বস্তু। তা কতকগুলো বস্তুকণার সমষ্টি। প্রতিটি কণাই অভিকর্ষ বল দ্বারা পৃথিবীর কেন্দ্রের দিকে আকৰ্ষিত হবে। এই সব বল মিলিত হয়ে একটি লব্ধি বল সৃষ্টি করবে। বস্তুটিকে ঘুরে ফিরে যেভাবেই রাখা হোক না কেন কণাগুলোর উপর পৃথিবীর আকর্ষণ বলের পরিমাণ, অভিমুখ ও ক্রিয়াবিন্দুর এবং সেই সঙ্গে ঐ বলগুলোর লন্দির পরিমাণ, অতিমুখ ও ক্রিয়াবিন্দুর কোন পরিবর্তন হবে না। এই লব্ধি বলই বস্তুর ওজন। [চিত্র ৭.১০]-এ ওজন বা বল বস্তুর 'G' বিন্দুর মধ্য দিয়ে ক্রিয়া করছে। এই বিন্দুই বস্তুটির অভিকর্ষ কেন্দ্র বা ভারকেন্দ্র।
ভরকেন্দ্র :
আমরা জানি একটি বস্তু অনেকগুলো বস্তুকণার সমষ্টি। বস্তুর কণাগুলোর সমস্ত ভরকে একটি মাত্র বিন্দুতে কেন্দ্ৰীভূত মনে করলে ঐ বিন্দুর মধ্য দিয়েই সমস্ত কণার উপর তাদের ভরের সমানুপাতিক ক্রিয়ারত সমান্তরাল বলসমূহের লন্ধি ক্রিয়া করে বলে বিবেচিত হয়। ঐ বিন্দুকে বস্তুর ভরকেন্দ্র বলে।
মনে করি : A একটি বস্তু। তা অনেকগুলো বস্তুকণার সমষ্টি। ধরি বস্তুকণাগুলোর ভর যথাক্রমে ,m1, m2, m3,……………. mn ইত্যাদি [চিত্র ৭.১১] সমস্ত ভরকে C বিন্দুতে সমবেত ধরা হলে ঐ ভরগুলোর উপর ক্লিয়ারত কণার ভরের সমানুপাতিক সমান্তরাল বলের লব্ধি C বিন্দুর মধ্য দিয়েই ক্রিয়া করবে। এই বিন্দুর নামই ভরকেন্দ্র।
গাণিতিক বিশ্লেষণের সাহায্যে কোনও তলে অবস্থিত বস্তুকণাসমূহের অভিকর্ষ কেন্দ্র নির্ণয় Determination of centre of gravity of particles in a plane by mathematical analysis
মনে করি A একটি বস্তু। এতে m1, m2, m3…….mn ভরবিশিষ্ট বস্তুকণা আছে। ধরি OX এবং OY সমকোণে অবস্থিত দুটি অক্ষ। এই অক্ষ দুটির সাপেক্ষে ধরি তাদের স্থানাংক যথাক্রমে (x1,y1 ), (x2 + y2), (x3, y3), (xn, yn) ইত্যাদি। মনে করি এদের ভারকেন্দ্র G বিন্দুতে অবস্থিত এবং এর স্থানাক () যেহেতু অবস্থিতির সঙ্গে ভারকেন্দ্রের রদ বদল হয় না, সেহেতু তলটি অনুভূমিক ধরা যেতে পারে। অতএব বস্তুকণাগুলোর ভার সমমুখী সমান্তরাল বল হবে এবং তারা উল্লম্বভাবে নিচের দিকে ক্রিয়া করবে। সংজ্ঞানুসারে G বিন্দুর মধ্য দিয়ে মোট ভার বা ওজন নিচের দিকে ক্রিয়া করবে। এখন Y-অক্ষ বরাবর ভারগুলোর মোমেন্টের গাণিতিক যোগফল ঐ অক্ষ বরাবর লম্বির মোমেন্টের সমান হবে।
(m1 g + m2 g + m3 g +.………+ mn g) = m1 gx1 + m2gx2+m3 gX3 +……..mn gxn
৭.১৪ ভরকেন্দ্র নির্ণয়
Determination of centre of mass
অসম অথবা সুষম বস্তুর ভারকেন্দ্র নিম্ন উপায়ে নির্ণয় করা যায় :
মনে করি একটি অসম ত্রিভুজাকৃতি পাতলা পাত ABC-এর ভারকেন্দ্র নির্ণয় করতে হবে। প্রথমে পাতটির যে কোন এক প্রান্ত, ধরা যাক, A-এ সুতা বেঁধে পাতটিকে ঝুলিয়ে আর একটি সুতায় একটি পাথরখণ্ড S বেঁধে ঐ একই প্রান্ত A হতে পাথরটিকে ঝুলিয়ে দেয়া হয় [চিত্র ৭.১৩]।
পাত ও পাথর খন্ডটির স্থিরাবস্থায় A হতে সুতা বরাবর পাতের উপর দিয়ে একটি সরলরেখা AD টানা হয়। অনুরূপভাবে পাতটিকে পর পর B ও C হতে ঝুলিয়ে পাতটির উপর দিয়ে সুতা বরাবর যথাক্রমে সরলরেখা BE ও CF টানা হয়। তাহলে, অঙ্কিত AD, BE ও CF-এর ছেদবিন্দু G-ই পাতটির ভারকেন্দ্র। কারণ স্থিরাবস্থায় সুতার টানের বিপরীতে বস্তুর ওজন ক্রিয়া করে এবং সুতাটি বস্তুর ভারকেন্দ্র দিয়ে যাবে। এখানে পাথরখণ্ডটি যে সুতায় ঝুলে থাকে তাকে ওলন সুতা এবং অঙ্কিত সরলরেখা গুলোকে ওলন রেখা বলা হয়।
৭:১৫ মহাকর্ষীয় ক্ষেত্র ও প্রাবল্য
Gravitational field and intensity
কোন বস্তুর চারদিকে যে স্থান জুড়ে তার আকর্ষণ বল অনুভূত হয়, সে স্থানকে উক্ত বস্তুর মহাকর্ষীয় ক্ষেত্র বলে।
মহাকর্ষীয় ক্ষেত্রের কোন বিন্দুতে একক ভরের কোন বস্তু স্থাপন করলে তার উপর যে বল প্রযুক্ত হয়, তাকে ঐ ক্ষেত্রের দরুন ঐ বিন্দুর মহাকর্ষীয় আকর্ষণ বলে। এটা সাধারণত মহাকর্ষীয় প্রাবল্য (Intensity)নামে পরিচিত। মনে করি M ভরের একটি বস্তু আছে। এই বস্তুর ভরকেন্দ্র হতে দূরে অবস্থিত কোন বিন্দুতে মহাকর্ষীয় প্রাবল্য নির্ণয় করতে হবে।
নিউটনের মহাকর্ষীয় সূত্র হতে আমরা জানি, M ও m ভরের দুটি বস্তুর ভরকেন্দ্র পরস্পর হতে দূরে থাকলে তাদের মধ্যে আকর্ষণ বলের পরিমাণ =
এখন যদি m= 1 একক হয়, তবে
বল = = M ভর কর্তৃক একক ভরের উপর M ভর অভিমুখী প্রযুক্ত বল। এটাই মহাকর্ষীয় প্রাবল্য E,
অর্থাৎ মহাকর্ষীয় প্রাবল্য, (28)
উক্ত সমীকরণ হতে সহজেই বুঝা যায় যে, M যত বেশি হবে, প্রাবল্যও তত বাড়বে। আবার r যত বেশি হবে, প্রাবল্য তত কমবে।
মহাকর্ষীয় ক্ষেত্রের বিভিন্ন বিন্দুতে প্রাবল্য বিভিন্ন হবে।
মহাকর্ষীয় ক্ষেত্রের কোন বিন্দুতে m ভরের একটি বস্তু রাখলে তার উপর ক্রিয়াশীল বল হবে,
যেহেতু বল একটি ভেক্টর রাশি, তাই মহাকর্ষীয় প্রাবল্য, একটি ভেক্টর রাশি। -এর দিক হবে -এর দিক বরাবর। অন্যভাবে বলা যায়, একক ভরের বস্তু যেদিকে বল লাভ করে -এর দিক সেদিকে হবে।
এম. কে. এস. ও আন্তর্জাতিক পদ্ধতিতে প্রাবল্যের একক নিউটন/কিলোগ্রাম (Nkg-1)।
৭'১৬. মহাকর্ষীয় বিভব
Gravitational potential
সংজ্ঞা : অসীম দূর হতে একক ভরের কোন বস্তুকে মহাকর্ষীয় ক্ষেত্রের কোন বিন্দুতে আনতে যে পরিমাণ কাজ সাধিত হয়, তাকে ঐ বিন্দুর মহাকর্ষীয় বিভব বলে।
একে সাধারণত V দ্বারা প্রকাশ করা হয়।
উল্লেখ্য, দুটি বস্তুর মধ্যে আকর্ষণ বলই কাজ করে থাকে। বাইরের কোন বল বা শক্তির প্রয়োজন হয় না। সুতরাং মহাকর্ষীয় বিভবকে ঋণ রাশি দ্বারা প্রকাশ করা হয় অর্থাৎ মহাকর্ষীয় ক্ষেত্রের কোন বিন্দুতে বিভব ঋণাত্মক এটা একটি স্কেলার রাশি।
এম. কে. এস. বা এস. আই. পদ্ধতিতে এর একক জুল/কিলোগ্রাম (Jkg-1)।
বিভব পার্থক্য (Potential difference) : একক ভরের কোন বস্তুকে মহাকর্ষীয় ক্ষেত্রের এক বিন্দু হতে অন্য বিন্দুতে আনতে যে পরিমাণ কাজ সাধিত হয়, তাকে ঐ বিন্দুর মধ্যে মহাকর্ষীয় বিভব পার্থক্য বলে।
আকর্ষণ বলের অভিমুখে সরণ হলে বিভব পার্থক্য ঋণাত্মক এবং আকর্ষণ বনের বিরুদ্ধে সরণ হলে বিভব পাৰ্থক্য ধনাত্মক হবে।
৭.১৭ বিন্দু ভরের দরুন মহাকর্ষীয় বিভব
Gravitational potential due to a point mass
আমরা জানি, অসীম দূরত্ব হতে একক ভরের কোন বস্তুকে মহাকর্ষীয় ক্ষেত্রের কোন বিন্দুতে আনতে যে পরিমাণ কাজ সাধিত হয়, তাকে উক্ত বিন্দুর মহাকর্ষীয় বিভব বলে।
এখন বিন্দু ভরের দরুন মহাকর্ষীয় বিভবের সাধারণ সমীকরণ বের করা যাক।
মনে করি, O বিন্দুতে M ভরের একটি বিন্দু ভর বস্তু অবস্থিত [চিত্র ৭-১৪]। O হতে দূরে P একটি বিন্দু। P বিন্দুতে মহাকর্ষীয় বিভব বের করতে হবে।
P বিন্দুতে একক ভরের উপর O বিন্দু অভিমুখী প্রযুক্ত বল অর্থাৎ মহাকর্ষীয় প্রাবল্য = । এখন একক ভরকে সামান্য দূরত্ব dr নিয়ে যেতে কাজের পরিমাণ অর্থাৎ বিভব,
dv = বল x সরণ = প্রাবল্য x সরণ =
একক ভরকে অসীম দূরত্ব হতে P বিন্দুতে আনতে কাজের পরিমাণ অর্থাৎ P বিন্দুতে বিভব
বা,
বা,
এখানে ঋণচিহ্ন এই অর্থ প্রকাশ করে যে, বাহ্যিক কোন বল বা শক্তি দ্বারা কাজ সম্পন্ন হয়নি, মহাকর্ষীয় বলই কাজ সম্পন্ন করেছে।
৭.১৮ প্রাবল্য ও বিভব পার্থক্যের মধ্যে সম্পর্ক
Relation between intensity and potential
মহাকর্ষীয় প্রাবল্য এবং মহাকর্ষীয় বিভবের মধ্যে সম্পর্ক স্থাপন করতে গিয়ে ধরি, A ও B মহাকর্ষীয় ক্ষেত্রে অবস্থিত কাছাকাছি দুটি বিন্দু [চিত্র ৭.১৫]। মনে করি এদের মধ্যবর্তী দূরত্ব । A বিন্দুর বিভব = VA এবং B বিন্দুর বিভব = VB। যেহেতু A ও B বিন্দু দুটি মহাকর্ষীয় ক্ষেত্রে কাছাকাছি অবস্থিত, সেহেতু বিন্দু দুটির মহাকর্ষীয় প্রাবল্য সমান ধরে নেয়া হয়। মনে করি এই প্রাবল্য = F
এখন, একক ভরের কোন বস্তুকে B বিন্দু হতে A বিন্দুতে আনতে কাজের পরিমাণ = প্রাবল্য × দূরত্ব
= F× AB = F×r
এটাই হল A বিন্দু এবং B বিন্দুর বিভব পার্থক্য অর্থাৎ (VA – VB)
F × AB=VA -VB
বা,
অর্থাৎ, দূরত্ব সাপেক্ষে বিভবের পরিবর্তনের হারকে প্রাবল্য বলে। ক্ষেত্রের অভিমুখে সরণ AB = dr হলে এবং A বিন্দুর বিভব V ও B বিন্দুর বিভব (V + dV) হলে, VA- VB =-dV
এটাই প্রাবল্য এবং বিভবের মধ্যে সম্পর্ক।
অতি প্রাচীনকাল হতে গ্রহ-নক্ষত্রের গতিবিধি সম্পর্কে বিজ্ঞানীদের যথেষ্ট আগ্রহ ছিল। ষোড়শ শতাব্দীতে ডেনমার্কের জ্যোতির্বিদ টাইকোব্রে (Tycho-Brahe) মংগল গ্রহের গতিবিধি লক্ষ করেন এবং কিছু তথ্য সংগ্রহ করেন। তাঁর এ গবেষণা লব্ধ তথ্য এবং অন্যান্য পর্যবেক্ষণের সাহায্যে 1618 খ্রিস্টাব্দে ডেনমার্কের অপর জ্যোতির্বিদ জন কেপলার (John Kepler) সিদ্ধান্তে উপনীত হন যে, গ্রহগুলো কোন এক বলের প্রভাবে সূর্যকে কেন্দ্র করে অবিরাম ঘুরছে। এই সম্পর্কে তিনি তিনটি সূত্র প্রদান করেন। তাঁর নাম অনুসারে এই তিনটি সূত্রকে কেপলার-এর গ্রহ সম্পৰ্কীয় গতিসূত্র (Kepler's laws of planetary motion) বলা হয়। সূত্র তিনটি নিম্নে আলোচিত হল ঃ
(১) উপবৃত্ত সূত্র (Law of ellipse) :
প্রতিটি গ্রহ সূর্যকে উপবৃত্তের নাভিতে বা ফোকাসে রেখে একটিউপবৃত্তাকার পথে প্রদক্ষিণ করছে।
(২) ক্ষেত্রফল সূত্র (Law of area) :
গ্রহ এবং সূর্যের সংযোগকারী ব্যাসার্ধ রেখা সমান সময়ে সমান ক্ষেত্রফল অতিক্রম করে।
(৩) সময়ের সূত্র (Law of time ) :
প্রতিটি গ্রহের পর্যায়কালের বর্গ সূর্য হতে তার গড় দূরত্বের ঘনফলের সমানুপাতিক।
ব্যাখ্যা :
১ম সূত্র :
এই সূত্র সূর্যের চারদিকে গ্রহের কক্ষপথের আকৃতি প্রকাশ করে। মনে করি S এবং একটি উপবৃত্তের দুটি নাভি। ধরি নাভিটি সূর্যের অবস্থিতি [চিত্র ৭.১৬]। কেপলারের প্রথম সূত্র অনুসারে যে কোন গ্রহ সূর্যকে s বিন্দুতে রেখে একটি উপবৃত্তাকার পথে ঘুরছে।
২য় সূত্র :
এই সূত্র কক্ষীয় বেগ এবং সূর্য ও গ্রহের মধ্যবর্তী দূরত্বের মধ্যে সম্পর্ক স্থাপন করে। মনে করি কোন গ্রহ। সময়ে P অবস্থান হতে Q অবস্থানে আসে। যদি একই সময়ে ঐ গ্রহ M অবস্থান হতে R অবস্থানে আসে, তবে কেপলারের দ্বিতীয় সূত্র হতে পাই, PQS-এর ক্ষেত্রফল এবং MSR-এর ক্ষেত্রফল সমান হবে।
৩য় সূত্র ঃ
এই সূত্র’গ্রহের কক্ষপথের আকার এবং অতিক্রান্ত সময়ের মধ্যে সম্পর্ক স্থাপন করে। মনে করি T গ্রহের পর্যায়কাল অর্থাৎ সূর্যকে একবার প্রদক্ষিণ করতে যে সময় লাগে তার মান T। যদি 2a পরাক্ষের দৈর্ঘ্য হয়, তবে কেপলারের তৃতীয় সূত্র হতে আমরা পাই,
যেহেতু 8 একটি ধ্রুব সংখ্যা, সেহেতু
উক্ত সমীকরণ হতে কেপলারের তৃতীয় সূত্রটিকে সামান্য পরিবর্তন করে নিম্নরূপে লিখা যায় -
প্রতিটি গ্রহের পর্যায়কালের বর্গ গ্রহের কক্ষপথের পরাক্ষের অর্ধেকের ঘন-এর সমানুপাতিক।
৭.২০ কেপলারের সূত্র হতে নিউটনের মহাকর্ষ সূত্র প্রতিপাদন
Derivation of newton's law of gravitation from Kepler's law
মহাবিজ্ঞানী নিউটন কেপলারের সূত্রগুলো ব্যাখ্যা করতে গিয়ে এই সিদ্ধান্তে উপনীত হলেন যে মহাবিশ্বে যে কোন দুটি বস্তু পরস্পরকে আকর্ষণ করে। সূর্যের চতুর্দিকে গ্রহগুলোর কক্ষপথ বৃত্তাকার গণ্য করে নিম্নলিখিত উপায়ে সহজে কেপলারের সূত্রগুলো হতে নিউটনের এই সিদ্ধান্তে উপনীত হওয়া যায়।
ধরা যাক m ভরের একটি গ্রহ সূর্যের চতুর্দিকে ব্যাসার্ধের বৃত্তপথে সমগতিতে ঘুরছে। কিন্তু গ্রহের উপর সূর্যের দিকে কেন্দ্রমুখী বল প্রয়োগ ব্যতীত গ্রহের এই বৃত্তাকার গতি সম্ভব নয়।
প্রয়োজনীয় কেন্দ্রমুখী বল
সূর্যের চতুর্দিকে গ্রহটির আবর্তন কাল T হলে,
কিন্তু কেপলারের তৃতীয় সূত্রানুসারে,
অর্থাৎ T2 = kr3, এখানে k একটি ধ্রুবক।
সুতরাং গ্রহের উপর সূর্যের আকর্ষণ বল, গ্রহের ভরের সমানুপাতিক এবং সূর্য হতে গ্রহের দূরত্বের বর্গের ব্যস্তানুপাতিক। কিন্তু প্রত্যেক ক্লিয়ার একটি সমান ও বিপরীত প্রতিক্রিয়া থাকে। কাজেই সমীকরণটিতে F-এর সাথে যেমন গ্রহের ভর m-এর সম্পর্ক আছে তদ্রূপ F-এ সূর্যের ভরেরও একই সম্পর্ক থাকবে। এজন্য -কে GM ধরা যায় ; এখানে G একটি ধ্রুবক এবং M সূর্যের ভর।
সূর্য ও গ্রহের মধ্যকার পারস্পরিক আকর্ষণ বল, (33)
এটাই নিউটনের মহাকর্ষীয় সমীকরণ। সুতরাং কেপলারের সূত্র হতে নিউটনের মহাকর্ষীয় সূত্র প্রতিষ্ঠিত হল।
৭.২১ মহাকর্ষীয় ভর এবং জড় ভর
Gravitational mass and inertial mass
পৃথিবী যে বল দ্বারা কোন বস্তুকে টানে তা বস্তুর ভরের সমানুপাতিক। এই ভর মহাকর্ষীয় তর। তুলাদণ্ডের সাহায্যে এই ভর নির্ণয় করা হয়। অন্য কথায় বলা যায়— তুলাদণ্ডে মেপে আমরা যে ভর নির্ণয় করি, তাই মহাকর্ষীয় ভর।
কোন বস্তুতে ধ্রুবমানের F বল প্রয়োগ করলে যদি তার ত্বরণ a হয়, তা হলে কে তার জড় তর বলে। পরীক্ষায় দেখা যায় উভয় ভর একই।'
৭.২২ মুক্তি বেগ
Escape velocity
আমরা জানি মহাকর্ষীয় বল কেন্দ্রগ বলে সংরক্ষণশীল। তাই কোন একটি বস্তুকে উপরের দিকে নিক্ষেপ করলে তা আবার মাটিতে এসে পড়ে। কিন্তু কোন বস্তুকে যদি এমন বেগে উর্ধ্বে উৎক্ষেপ করা হয় যে তা পৃথিবীর অভিকর্ষীয় ক্ষেত্র অতিক্রম করে যায় তবে বস্তুটি আর কখনই পৃথিবীর পৃষ্ঠে ফিরে আসবে না। ন্যূনতম এই বেগকে মুক্তি বেগ বলে। অতএব কোন বস্তুকে ন্যূনতম যে বেগে ঊর্ধ্বে উৎক্ষেপ করলে তা আর পৃথিবী পৃষ্ঠে ফিরে আসে না তাকে মুক্তি বেগ বা পলায়ন বেগ বা নিষ্ক্রমণ বেগ বলে। একে VE দ্বারা সূচিত করা হয়।
মুক্তি বেগের সমীকরণ বের করতে গিয়ে ধরি উৎক্ষিপ্ত বস্তুর ভর m, পৃথিবীর ভর M, পৃথিবীর ব্যাসার্ধ R, পৃথিবীর কেন্দ্র হতে বস্তুর দূরত্ব r, [চিত্র ৭.১৭] অতএব বস্তুর উপর অভিকর্ষ বল,
এখন বস্তুটি যদি অভিকর্ষ বলের বিরুদ্ধে dr পরিমাণ উপরে উঠে, তবে কাজের পরিমাণ, dW = F.dr
সুতরাং অভিকর্ষীয় বল ছাড়াতে বস্তুটিকে মোট যে পরিমাণ কাজ করতে হবে, তার মান
বা,
অর্থাৎ,
মনে করি, বস্তুর উৎক্ষিপ্ত বেগ = VE । তা হলে তার প্রাথমিক গতিশক্তি
এই শক্তি ব্যয় করেই বস্তুটি অভিকর্ষীয় ক্ষেত্রের সীমানা ছাড়িয়ে যায় অর্থাৎ উপরোক্ত কাজ করবে।
:-
এটাই হল যুক্তি বেগের সমীকরণ। উপরোক্ত সমীকরণে m না থাকায় আমরা বলতে পারি যে, মুক্তি বেগ বস্তুর ভরের উপর নির্ভর করে না। বস্তু ছোট বা বড় যাই হোক না কেন, মুক্তি বেগ একই হবে।
উদাহরণস্বরূপ ধরা যায়, পৃথিবীর ব্যাসার্ধ,
R = 64 x 105m ও g = 9.80 ms-2
অতএব এক্ষেত্রে মুক্তি বেগ,
= 11.20Kms-1 = 7 মাইল/সে. (প্রায় )
= 25000 মাইল/ঘন্টা
সুতরাং কোন বস্তুকে যদি প্রতি ঘণ্টায় 25000 মাইল বেগে বা এর অপেক্ষা অধিক বেগে উৎক্ষেপ করা হয়, তবে তা আর ভূ-পৃষ্ঠে ফিরে আসে না।
বিশেষ দ্রষ্টব্য : পৃথিবী পৃষ্ঠ হতে কোন বস্তুকে বেগে উপর দিকে নিক্ষেপ করলে পৃথিবীর আকর্ষণ বলের দ্বারা বস্তুটির বিভিন্ন পরিণতি হতে পারে। যথা ঃ
(১) যদি - হয়, অর্থাৎ উৎক্ষেপণ বেগ 7.88 kms-1 অপেক্ষা কম হয়, তবে তা উপবৃত্তাকার পথে পৃথিবী প্রদক্ষিণ করবে এবং অবশেষে পৃথিবীতে ফিরে আসবে [চিত্র ৭.১৮-এ (ক)]।
(২) যদি -হয় অর্থাৎ উৎক্ষেপণ বেগ 7.88 kms-1 হয়, তবে বস্তুটি বৃত্তাকার পথে পৃথিবীকে প্রদক্ষিণ করবে এবং চাঁদের মত উপগ্রহে পরিণত হবে [চিত্র ৭.১৮-এ (খ)।
৩) যদি কিন্তু
(৪) যদি v =VE হয়, অর্থাৎ উৎক্ষেপণ বেগ 11.2 kms-1 অর্থাৎ মুক্তি বেগের সমান হয়, তবে বস্তুটি একটি অধিবৃত্ত পথে পৃথিবী পৃষ্ঠ ছেড়ে যায় এবং তা পৃথিবীর আকর্ষণ ক্ষেত্র অতিক্রম করে বাইরে চলে যাবে [চিত্র ৭.১৮-এ (ঘ)]।
(৫) যদি V>VE হয়, অর্থাৎ উৎক্ষেপণ বেগ মুক্তি বেগ অপেক্ষা বেশি হয়, তবে বস্তু পরাবৃত্ত পথে পৃথিবী-পৃষ্ঠ ছেড়ে যায় এবং তা আর পৃথিবীতে ফিরে আসে না [চিত্র ৭.১৮-এ (ঙ)]।
# বহুনির্বাচনী প্রশ্ন
সূচনা :
আমরা জানি সূর্য ও তার চারদিকের গ্রহ, উপগ্রহ, উল্কা, নীহারিকা ইত্যাদি নিয়ে যে জগৎ তার নাম সৌরজগৎ। সৌরজগতের কেন্দ্রে থাকে সূর্য। আর গ্রহগুলো সূর্যকে কেন্দ্র করে তার চারদিক প্রদক্ষিণ করছে। গ্রহগুলোকে কেন্দ্র করে উপগ্রহগুলো তাদের চারদিকে ঘুরছে। যেমন পৃথিবী একটি গ্রহ। এটি সূর্যের চারদিকে ঘুরছে। চন্দ্র পৃথিবীর একটি উপগ্রহ। চন্দ্র পৃথিবীর চারদিক প্রদক্ষিণ করছে।
স্বাভাবিক উপগ্রহ :
যে সব বস্তু বা জ্যোতিষ্ক গ্রহের চারদিকে ঘোরে, তাদেরকে উপগ্রহ বলে। যে সব উপগ্রহ প্রাকৃতিক কারণে সৃষ্ট তাদেরকে স্বাভাবিক উপগ্রহ বলে। যেমন চন্দ্র প্রাকৃতিক কারণে সৃষ্টি হয়েছে। এটি পৃথিবীর চারদিকে ঘুরছে। অতএব চন্দ্র বা চাঁদ পৃথিবীর একটি স্বাভাবিক উপগ্রহ। তেমনি অন্যান্য গ্রহগুলোর ও স্বাভাবিক উপগ্রহ রয়েছে।
কৃত্রিম উপগ্রহ :
আমরা জানি সৌরজগৎ নামে একটি জগৎ রয়েছে যার কেন্দ্রে থাকে সূর্য। সূর্য হতে ছিটকে আসা কতকগুলো জ্যোতিষ্ক সূর্যকে প্রদক্ষিণ করছে। এদের নাম গ্রহ (planet)। পৃথিবী সূর্যের একটি গ্রহ। পুনঃ, গ্রহ হতে ছিটকে আসা কতকগুলো জ্যোতিষ্ক গ্রহগুলোকে প্রদক্ষিণ করছে। এদের নাম উপগ্রহ (satellite)। চাঁদ পৃথিবীর একটি উপগ্রহ যা প্রায় ৩০ দিনে পৃথিবীকে একবার প্রদক্ষিণ করে। সৃষ্টির আদিকাল থেকেই মানুষের মনে কৌতূহল জাগছে কি করে চাঁদ পৃথিবীর চারদিকে ঘুরছে। এই প্রশ্নের জবাবে বিজ্ঞানীরা বলেছেন অভিকর্ষের দরুন চাঁদের উপর পৃথিবীর কেন্দ্রমুখী বল এর কারণ। এই কেন্দ্রমুখী বল যদি না থাকত, তাহলে চাঁদ মহাশূন্যে মিলিয়ে যেত। পৃথিবীর চারদিকে চাদের প্রদক্ষিণের দরুন সৃষ্ট কেন্দ্রবিমুখী বল পৃথিবী কর্তৃক প্রযুক্ত কেন্দ্রমুখী বলের সমান ও বিপরীত হওয়ায় চাঁদ সোজা না গিয়ে পৃথিবীর চারদিকে বৃত্তাকার পথে ঘুরছে। এই তত্ত্বের উপর ভিত্তি করে মানুষ মহাশূন্যে পাড়ি দেয়ার জন্যে যে উপগ্রহ তৈরি করেছে, তার নাম কৃত্রিম উপগ্রহ।
1957 সালের 4th অক্টোবর রাশিয়ার বিজ্ঞানীরা সর্বপ্রথম মহাশূন্যে একটি কৃত্রিম উপগ্রহ পাঠান। এর নাম স্পুটনিক-1। সে বছরেই আরো একটি কৃত্রিম উপগ্রহ মহাশূন্যে পাঠান হয়। এর নাম স্পুটনিক-2। এই সময় আমেরিকার বিজ্ঞানীরা পেছনে ছিলেন না। তাঁরাও 1958 সালে মহাশূন্যে একটি কৃত্রিম উপগ্রহ উৎক্ষেপণ করেন। এর নাম এক্সপ্লোরার-1। এমনিভাবে মহাশূন্যে কৃত্রিম উপগ্রহ পাঠিয়ে পৃথিবী তথা সৌরজগতের নানা রকম রহস্য উদঘাটনের কাজ চলছে। রাশিয়ার বিখ্যাত বিজ্ঞানী ইউরি গ্যাগারিন ভস্টক-1 কৃত্রিম উপগ্রহের সাহায্যে সর্বপ্রথম মহাশূন্যে বিচরণ করেন।
পরীক্ষার সাহায্য দেখা গেছে যে কোন একটি বস্তুকে পৃথিবী পৃষ্ঠ থেকে প্রায় 930 km উপরে তুলে 8:05 kms-1 হতে 11*1 kms-1 বেগে মহাশূন্যে উৎক্ষেপণ করলে তা পৃথিবীর একটি কৃত্রিম উপগ্রহ হিসেবে চাঁদের মত পৃথিবীকে প্রদক্ষিণ করবে। কিন্তু কোন বস্তুকে এত উপরে তুলে এত বেশি বেগ দেয়া সম্ভব নয়। কারণ বায়ুস্তরের সাথে এর ঘর্ষণে এত অধিক তাপ উৎপন্ন হবে যে কৃত্রিম উপগ্রহটি পুড়ে ভস্মীভূত হবে। তাই বায়ুতে এত বেশি বেগ না দিয়ে বায়ুস্তর অতিক্রম করার পর কৃত্রিম উপগ্রহে এত বেশি বেগ প্রদান করা হয় এবং তা প্রদান করা হয় একটি রকেটের সাহায্যে তিনটি ধাপে। কৃত্রিম উপগ্রহটি বসানো হয় রকেটের নাকের ডগায় এবং জ্বালানি ও অন্যান্য যন্ত্রপাতি বসানো হয় রকেটের ভেতরে। ধাপগুলো নিম্নরূপ :
সবচেয়ে নিচু স্তুরের রকেটটি সর্বপ্রথমে কাজ শুরু করে। এটি উপগ্রহ ও অপর দুটি স্তরের রকেটসহ খানিকটা খাড়া উপরে উঠে আস্তে আস্তে বাঁক নিতে থাকে। এই ধাপ প্রয়োজনীয় বেগের অংশ যোগানের পর খসে পড়ে। এই সময় দ্বিতীয় ধাপ কাজ শুরু করে এবং এই ধাপটি উপগ্রহটির বেগের প্রায় অংশ যোগানোর পর খসে পড়ে। তার পর শুরু হয় তৃতীয় ধাপের কাজ। এই ধাপটি উপগ্রহটিতে প্রয়োজনীয় বেগ প্রদান করে নিজে খসে পড়ে। উপগ্রহটি তখন পৃথিবী প্রদক্ষিণ করতে শুরু করে।
৭:২৪ বৃত্তাকার পথে পৃথিবী প্রদক্ষিণ কালে কৃত্রিম উপগ্রহের কক্ষীয় বেগ, আবর্তন কাল এবং উচ্চতার রাশিমালা
Expression for orbital velocity, time period and height of an artificial satellite rotating around the earth in a circular path
(ক) বেগ ঃ
মনে করি m ভরের একটি কৃত্রিম উপগ্রহ পৃথিবী পৃষ্ঠ হতে h উচ্চতায় অবস্থান করে v বেগে বৃত্তাকার পথে প্রদক্ষিণ করছে। এখানে উপগ্রহটির উপর পৃথিবীর আকর্ষণ বল = উপগ্রহটির ঘূর্ণনের জন্য প্রয়োজনীয় কেন্দ্রমূখী বল।
মনে করি পৃথিবীর ভর M এবং এর ব্যাসার্ধ R।
উপগ্রহটির উপর পৃথিবীর আকর্ষণ বল
এটি পৃথিবীর কেন্দ্রাভিমুখী ক্রিয়া করছে। পুনঃ, উপগ্রহটির ঘূর্ণনের জন্য প্রয়োজনীয় কেন্দ্ৰমুখী বল
গতির সাম্যাবস্থা হতে পাই
বা,
:-
এটিই হল h উচ্চতায় উপগ্রহটির প্রদক্ষিণ বেগ ।
উল্লেখ্য কক্ষপথের ব্যাসার্ধ কম হলে বেগ কম হবে। শুধু তাই নয় সমীকরণে m না থাকায় উপগ্রহটির বেগ এর ভরের উপর নির্ভর করে না।
(খ) আবর্তনকাল বা পর্যায়কাল :
মনে করি কৃত্রিম উপগ্রহটির আবর্তন বা পর্যায়কাল = T, যদি উপগ্রহটির কৌণিক বেগ হয়, তবে
বৃত্তাকার পথের ব্যাসার্ধ
বা,
বা,
বা,
উক্ত সমীকরণে v এর মান বসিয়ে পাই
বা,
এটিই হল কৃত্রিম উপগ্রহের আবর্তন কালের রাশিমালা।
(গ) কৃত্রিম উপগ্রহের উচ্চতা :
মনে করি পৃথিবী পৃষ্ঠ হতে কৃত্রিম উপগ্রহের উচ্চতা = h সমীকরণ (40)-এর উভয় পার্শ্বকে বর্গ করে পাই
বা,
এটিই হল কৃত্রিম উপগ্রহের উচ্চতার রাশিমালা এবং আবর্তনকান ও উচ্চতার মধ্যে সম্পর্ক।
৭:২৫, ভূ-স্থির উপগ্রহ
Geostationary satellite
আমরা জানি পৃথিবী 24 ঘণ্টায় তার অক্ষের চারদিকে একবার ঘুরে আসে। এর নাম আহ্নিক গতি যার ফলে দিবা-রাত্র হয়। কোন কৃত্রিম গ্রহের আবর্তন কাল এবং নিজ অক্ষের চারদিকে ঘূর্ণায়মান পৃথিবীর আবর্তন কাল সমান হলে পৃথিবী পৃষ্ঠের একজন পর্যবেক্ষকের কাছে একে সব সময়ই স্থিতিশীল মনে হবে। পৃথিবীর যে স্থানের খাড়া উপর থেকে একে বৃত্তাকার কক্ষপথে স্থাপন করা হয় এটি পৃথিবীর ঐ স্থানের উপরই সব সময় স্থিতিশীল আছে বলে মনে হবে। এর নামই ভূ-স্থির উপগ্রহ এবং যে কক্ষপথে কৃত্রিম উপগ্রহ স্থিতিশীল থাকে তাকে পার্কিং (parking) কক্ষপথ বলে।
সংজ্ঞা : কোন কৃত্রিম উপগ্রহের আবর্তনকাল নিজ অক্ষের চারদিকে ঘূর্ণায়মান পৃথিবীর আবর্তনকালের সমান হলে পৃথিবী সাপেক্ষে এটি স্থির থাকবে। এই ধরনের উপগ্রহকে ভূ-স্থির উপগ্রহ বলে। ভূ-স্থির উপগ্রহের কক্ষপথকে পার্কিং কক্ষপথ বলে।
মনে করি পৃথিবীর কেন্দ্রের সাথে এককেন্দ্রিক ভাবে নিরক্ষতলে (In the plane of equator) m ভরের একটি কৃত্রিম উপগ্রহ পৃথিবীর চারদিকে ঘুরছে। উপগ্রহের কক্ষপথের ব্যাসার্ধ এবং কক্ষপথে উপগ্রহের গতিবেগ এর উপর কেন্দ্রমুখী বা কেন্দ্রবিমুখী বল (42)
পুনঃ, পৃথিবীর ভর M হলে মহাকর্ষীয় বল
F = F'
বা,
কিন্তু অভিকর্ষীয় ত্বরণ
বা,
যদি কৃত্রিম উপগ্রহের কক্ষপথ বরাবর আবর্তন কাল T হয়, তবে
এখন কৃত্রিম উপগ্রহের আবর্তন কাল এবং পৃথিবীর নিজ অক্ষের চারদিকের আবর্তন কাল সমান হলে পৃথিবী থেকে উপগ্রহটিকে একই স্থানে স্থির দেখা যায়। এর নাম ভূ-স্থির উপগ্রহ এবং ঐ কক্ষপথের নাম পার্কিং কক্ষপথ । উল্লেখ্য, পার্কিং কক্ষপথে রিলে উপগ্রহ স্থাপন করে পৃথিবীর এক স্থানের সংবাদ, খেলাধূলা, বিভিন্ন অনুষ্ঠান ইত্যাদি পৃথিবীর অন্য স্থানে ধারাবাহিকভাবে দেখানো যায়।
৭.২৬ কৃত্রিম উপগ্রহের ব্যবহার
Uses of artificial satellite
আধুনিক বিজ্ঞানের যুগে কৃত্রিম উপগ্রহের বহুল ব্যবহার রয়েছে। ব্যবহারগুলো নিচে উল্লেখ করা হল ঃ
(১) পৃথিবীর আকার ও আকৃতি সম্পর্কিত ভূ-জরিপ করা যায়।
(২) এর সাহায্যে ভূ-পৃষ্ঠের এলাকা সম্পর্কে বেতার ও টেলিভিশনের মাধ্যমে তথ্য প্রদান করা যায়।
(৩) উচ্চ বায়ুমণ্ডলের চাপ, তাপমাত্রা বা গঠন নির্ণয় করা যায়।
(৪) ঊর্ধ্বাকাশের আয়নমণ্ডল, কসমিক বিকিরণ, চার্জিত কণিকার ভ্যান আসেল বেষ্টনী, সৌর বিকিরণের প্রভাব ইত্যাদি সম্পর্কে তথ্য সংগ্রহ করা যায়।
(৫) আবহাওয়া সম্পর্কীয় নিরীক্ষণ ও পূর্বাভাস পাওয়া যায় ।
(৬) বহির্বিশ্বে রনজেন রশ্মি, গামারশ্মি ইত্যাদির উৎস সংক্রান্ত ও জ্যোতির্বিজ্ঞানের অন্যান্য গবেষণা চালানো যায়।
(৭) প্রতিরক্ষামূলক পাহারা ও বিভিন্ন সামরিক ব্যবস্থায় এটি ব্যবহৃত হয়।
(৮) আন্তমহাদেশীয় যোগাযোগে এটি ব্যবহার করা হয়।
(৯) পৃথিবীর যে-কোন দেশে অনুষ্ঠিত খেলাধূলা বা যে-কোন অনুষ্ঠান ধারাবাহিকভাবে টেলিভিশনের মাধ্যমে দেখানো হয়।
(১০) কৃত্রিম উপগ্রহের সাহায্যে সমুদ্রের গভীরতা নির্ণয় করা যায়।
মহাশূন্যচারীর ওজনহীনতা :
আমরা জানি, ওজন, W = mg। অর্থাৎ, ভর x অভিকর্ষ ত্বরণের গুণফল হল ওজন। বস্তুর ভর নির্দিষ্ট। মানুষের ভরও নির্দিষ্ট। কিন্তু g-এর মান তারতম্য হলে ওজন কম-বেশি হয়।
মহাশূন্যচারীরা খেয়াযানে পৃথিবী থেকে একটি নির্দিষ্ট উচ্চতার বৃত্তাকার পথে প্রদক্ষিণ করে। এই বৃত্তাকার গতির জন্য পৃথিবীর কেন্দ্রের দিকে ঐ উচ্চতায় অভিকর্ষজ ত্বরণের মানের সমান মানের একটি ত্বরণ সৃষ্টি হয়। ফলে এই মহাশূন্য যানের' দেওয়াল বা পাটাতনের সাপেক্ষে মহাশূন্যচারীর ত্বরণ (g - g) = 0 হয়। তাই মহাশূন্যচারীর
ওজন W = m x 0 = 0।
প্রত্যেক গ্রহ সূর্যকে কেন্দ্র করে মোটামুটি বৃত্তাকার কক্ষপথে সূর্যের চতুর্দিকে পরিভ্রমণ করছে। গ্রহের উপর সূর্যের মহাকর্ষীয় আকর্ষণ বল হতে প্রয়োজনীয় কেন্দ্রমুখী বলের উদ্ভব হয়।
ধরা যাক m ভরের একটি গ্রহ সূর্যকে কেন্দ্র করে । ব্যাসার্ধের বৃত্তপথে য় সমদ্রুতিতে পরিভ্রমণ করছে এবং ভর M; তা হলে তাদের মধ্যে পারস্পরিক আকর্ষণ
গ্রহের বৃত্তাকার গতির জন্য প্রয়োজনীয় কেন্দ্রমুখী বল,
:-
বা,
গ্রহটি সূর্যের চতুর্দিকে T সময়ে একবার পরিভ্রমণ করলে,
T এবং r জানা থাকলে সূর্যের ভর M নির্ণয় করা যায়।
সূর্যের ভর :
পৃথিবী সূর্যের চারদিকে পরিভ্রমণ করছে। পৃথিবীর পর্যায়কাল T প্রায় 365 দিন = 365 x 24 x 60 x 60 সেকেন্ড এবং পৃথিবীর কেন্দ্র থেকে সূর্যের দূরত্ব = 1.5 x 1011 m।
সমীকরণ (47)-এ মানগুলো বসিয়ে আমরা পাই।
সূর্যের ভর,
=2 ×1030 kg
মহাকর্ষ :
নভোমণ্ডলে অবস্থিত দুটি বস্তু বা বস্তুকণার মধ্যকার পারস্পরিক আকর্ষণ বলকে মহাকর্ষ বলে।
অভিকর্ষ বা মাধ্যাকর্ষণ :
পৃথিবী এবং অন্য একটি বস্তু বা বস্তুকণার মধ্যকার আকর্ষণ বলকে অভিকর্ষণ বা মাধ্যাকর্ষণ বলে।
নিউটনের মহাকর্ষ সূত্র :
মহাবিশ্বের যে কোন দুটি বস্তুকণা পরস্পরকে আকর্ষণ করে। এই আকর্ষণ বল বস্তু দুটির ভরের গুণফলের সমানুপাতিক, তাদের দূরত্বের বর্গের ব্যস্তানুপাতিক এবং বস্তু দুটির সংযোগকারী সরলরেখা বরাবর ক্রিয়াশীল।
মহাকর্ষীয় ধ্রুবক, G :
একক ভরবিশিষ্ট দুটি বস্তুকণা একক দূরত্বে থেকে যে পরিমাণ বল দ্বারা পরস্পরকে আকর্ষণ করে তার সংখ্যাগত মানকে মহাকর্ষীয় ধ্রুবক বলে। একে G দ্বারা প্রকাশ করা হয়।
অভিকর্ষজ বা অভিকর্ষীয় ত্বরণ :
কোন স্থানে অভিকর্ষের টানে মুক্তভাবে পড়ন্ত বস্তুর বেগ যে হারে বৃদ্ধি পায় তাকে ঐ স্থানের অভিকর্ষজ বা অভিকর্ষীয় ত্বরণ বলে। অথবা, বস্তুতে অভিকর্ষ বল কর্তৃক যে ত্বরণ উৎপন্ন হয় তাকে অভিকর্ষজ ত্বরণ বলে।
ভর :
কোন একটি বস্তুতে যে পরিমাণ পদার্থ আছে, তাকে তার ভর বলে।
ওজন :
কোন একটি বস্তু যে পরিমাণ বল দ্বারা পৃথিবীর কেন্দ্রের দিকে আকৃষ্ট হয় তাকে তার ওজন বলে।
অভিকর্ষ কেন্দ্র বা ভারকেন্দ্র :
বস্তুকে যেভাবেই রাখা হোক না কেন তার ওজন যে বিশেষ বিন্দুর মধ্য দিয়ে বস্তুর ওপর সর্বদা ক্রিয়া করে ঐ বিন্দুকে অভিকর্ষ কেন্দ্র বা ভারকেন্দ্র বলে।
ভরকেন্দ্র :
বস্তুর কণাগুলোর সমস্ত ভরকে একটি মাত্র বিন্দুতে কেন্দ্রীভূত মনে করলে ঐ বিন্দুর মধ্য দিয়ে সমস্ত কণার ওপর তাদের ভরের সমানুপাতিক ক্রিয়ারত সমান্তরাল বলসমূহের লব্ধি ক্রিয়া করে বলে বিবেচিত হয়। ঐ বিন্দুকে বস্তুর ভরকেন্দ্র বলে।
মহাকর্ষীয় প্রাবল্য :
মহাকর্ষীয় ক্ষেত্রের কোন বিন্দুতে একক ভরের কোন বস্তু স্থাপন করলে তার উপর যে বল প্রযুক্ত হয় তাকে মহাকর্ষীয় প্রাবল্য বলে।
মহাকর্ষীয় বিভব ঃ
অসীম দূর থেকে একক ভরের কোন বস্তুকে মহাকর্ষীয় ক্ষেত্রের কোন বিন্দুতে আনতে যে পরিমাণ কাজ সাধিত হয়, তাকে ঐ বিশুর মহাকর্ষীয় বিভব বলে।
কেপলার-এর সূত্র ঃ
(১) উপবৃত্ত সূত্র ঃ
প্রতিটি গ্রহ সূর্যকে উপবৃত্তের নাভিতে রেখে একটি উপবৃত্তাকার পথে প্রদক্ষিণ করছে।
(২) ক্ষেত্রফল সূত্র ঃ
গ্রহ এবং সূর্যের সংযোগকারী ব্যাসার্ধ রেখা সমান সময়ে সমান ক্ষেত্রফল অতিক্রম করে।
(৩) সময়ের সূত্র ঃ
প্রতিটি গ্রহের পর্যায় কালের বর্গ সূর্য হতে তার গড় দূরত্বের ঘনফলের সমানুপাতিক।
মুক্তি বেগ ঃ
কোন বস্তুকে ন্যূনতম যে বেগে উর্ধ্বে উৎক্ষেপ করলে তা আর পৃথিবী পৃষ্ঠে ফিরে আসে না তাকে মুক্তি বেগ বলে।
ভূ-স্থির উপগ্রহ ঃ
কোন কৃত্রিম উপগ্রহের আবর্তনকাল নিজ অক্ষের চারদিকে ঘূর্ণায়মান পৃথিবীর আবর্তনকালের সমান হলে পৃথিবী সাপেক্ষে এটি স্থির থাকবে। এ ধরনের উপগ্রহকে ভূ-স্থির উপগ্রহ বলে।
পার্কিং কক্ষপথ :
ভূ-স্থির উপগ্রহের কক্ষপথকে পার্কিং কক্ষপথ বলে।